语言模型
自然语言处理是关于计算机科学和语言学的交叉学科,常见的研究任务包括:
- 分词(Word Segmentation或Word Breaker,WB)
- 信息抽取(Information Extraction,IE):命名实体识别和关系抽取(Named Entity Recognition & Relation Extraction,NER)
- 词性标注(Part Of Speech Tagging,POS)
- 指代消解(Coreference Resolution)
- 句法分析(Parsing)
- 词义消歧(Word Sense Disambiguation,WSD)
- 语音识别(Speech Recognition)
- 语音合成(Text To Speech,TTS)
- 机器翻译(Machine Translation,MT)
- 自动文摘(Automatic Summarization)
- 问答系统(Question Answering)
- 自然语言理解(Natural Language Understanding)
- OCR
- 信息检索(Information Retrieval,IR)
语言模型与应用
上个世纪80年代后期,机器学习算法被引入到自然语言处理中,这要归功于不断提高的计算能力。
研究主要集中在统计模型上,这种方法采用大规模的训练语料(corpus)对模型的参数进行自动的学习,和之前的基于规则的方法相比,这种方法更具鲁棒性。
语言模型
语言模型简单来讲,就是计算一个句子的概率,更确切的说是计算组成这个句子一系列词语的概率。
对一句话𝑆=𝑥1,𝑥2,𝑥3,𝑥4,𝑥5,…,𝑥𝑛S=x1,x2,x3,x4,x5,…,xn而言,它的概率
𝑃(𝑆)=𝑃(𝑥1,𝑥2,𝑥3,𝑥4,𝑥5,…,𝑥𝑛)=𝑃(𝑥1)𝑃(𝑥2|𝑥1)𝑃(𝑥3|𝑥1,𝑥2)...𝑃(𝑥𝑛|𝑥1,𝑥2,...,𝑥𝑛−1)
联合概率链规则公式考虑到了所有的词和词之间的依赖关系,但是非常复杂。使用马尔科夫假设(Markov Assumption)简化:下一个词的出现仅依赖于它前面的一个或几个词。
二元语法(bigram,2-gram):
\(P(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10})=P(x_1)P(x_2|x_1)P(x_3|x_2)P(x_4|x_3)..P(x_{10}|x_9)\)
三元语法(trigram,3-gram):
𝑃(𝑥1,𝑥2,𝑥3,𝑥4,𝑥5,𝑥6,𝑥7,𝑥8,𝑥9,𝑥10)=𝑃(𝑥1)𝑃(𝑥2|𝑥1)𝑃(𝑥3|𝑥1,𝑥2)𝑃(𝑥4|𝑥2,𝑥3)×...×𝑃(𝑥10|𝑥8,𝑥9)
为什么叫“语言模型”?因为这是统计学意义上的模型,又跟语言相关,所以叫语言模型。统计模型指一系列分布,参数模型指一系列可用有限个参数表示的模型。语言模型就是一种参数模型,它的参数是矩阵的所有cell。
选择N-gram的N
理论上,只要有足够大的语料,n越大越好,毕竟这样考虑的信息更多
条件概率为统计计数:
𝑃(“优惠”|“发票”,“点数”)= (“发票”,“点数”,“优惠”) 出现的次数 / (“发票”,“点数”)出现的次数
- 实际情况往往是训练语料很有限,很容易产生数据稀疏,不满足大数定律,算出来的概率失真。比如(“发票”,“点数”,“优惠”)在训练集中竟没有出现,就会导致零概率问题。
大数定律:样本数量越多,其算术平均值就越趋近期望值。
- 另一方面,如果n很大,参数空间过大,产生维数灾难。假设词表的大小为100000,那么n-gram模型的参数数量为\(100000^n\)。这么多的参数,估计内存就不够放了。
如何选择依赖词的个数n呢?
- 经验上,trigram用的最多。尽管如此,原则上,能用bigram解决,绝不使用trigram。n取≥4的情况较少。
- 当n更大时:对下一个词出现的约束信息更多,具有更大的辨别力;
- 当n更小时:在训练语料库中出现的次数更多,具有更可靠的统计信息,具有更高的可靠性、实用性。
N-gram语言模型应用
词性标注
词性标注是一个典型的多分类问题。
“爱”作为动词还是比较常见的。所以可以统一给“爱”分配为“动词”。这种最简单的思想非常好实现,如果准确率要求不高则也比较常用。它只需要基于词性标注语料库做一个统计就够了,连贝叶斯方法、最大似然法都不要用。
可以引入2-gram模型提升匹配的精确度。
𝑃(词性𝑖|“很”的词性(副词),“爱") = 前面被“副词”修饰的“爱"作为“词性𝑖”的次数 / 前面被“副词”修饰的“爱"出现的次数;𝑖=1,2,3...
垃圾邮件识别
一个可行的思路如下:
- 先对邮件文本进行断句,以句尾标点符号(“。” “!” “?”等)为分隔符将邮件内容拆分成不同的句子。
- 用N-gram分类器判断每个句子是否为垃圾邮件中的敏感句子。
- 当被判断为敏感句子的数量超过一定数量(比如3个)的时候,认为整个邮件就是垃圾邮件。
根据贝叶斯公式有:
𝑃(𝑌𝑖|𝑋)∝𝑃(𝑋|𝑌𝑖)𝑃(𝑌𝑖);𝑖=1,2
对𝑃(𝑋|𝑌𝑖)P(X|Yi) 套用2-gram模型。 则上式化简为:
𝑃(𝑌𝑖|𝑋)∝𝑃(𝑋|𝑌𝑖)𝑃(𝑌𝑖) ∝𝑃(𝑥1|𝑌𝑖)𝑃(𝑥2|𝑥1,𝑌𝑖)𝑃(𝑥3|𝑥2,𝑌𝑖)...𝑃(𝑥10|𝑥9,𝑌𝑖)𝑃(𝑌𝑖)
因为这种方法考虑到了词语前面的一个词语的信息,同时也考虑到了部分语序信息,因此区分效果会比单纯用朴素贝叶斯方法更好。
N-gram方法在实际应用中有一些tricks
- 从区分度来看,3-gram方法更好些。
- 可以考虑在其前面再添加一个句子起始符号如“<𝑠>”,这样我们就不必单独计算𝑃(“我”|𝑌𝑖),而是替换为计算𝑃(“我”|“<𝑠>”,𝑌𝑖)。形式上与2-gram统一。 这样统计和预测起来都比较方便。(一般地,如果采用N-gram模型,可以在文本开头加入n-1个虚拟的开始符号)
- N-gram模型也会发生零概率问题,也需要平滑技术
中文分词
中文分词技术是“中文NLP中,最最最重要的技术之一”,重要到某搜索引擎厂有专门的team在集中精力优化这一项工作,重要到能影响双语翻译百分位的准确度,能影响某些query下搜索引擎百分位的广告收入。
中文分词也可以理解成一个多分类的问题。𝑋表示被分词的句子,用𝑌𝑖表示该句子的一个分词方案。
𝑃(𝑌𝑖|𝑋)∝𝑃(𝑋|𝑌𝑖)𝑃(𝑌𝑖);𝑖=1,2,3...
NOTE:任意假想的一种分词方式之下生成的句子总是唯一的(只需把分词之间的分界符号扔掉剩下的内容都一样)。于是可以将 𝑃(𝑋|𝑌𝑖)看作是恒等于1的。这样贝叶斯公式又进一步化简成为:
𝑃(𝑌𝑖|𝑋)∝𝑃(𝑌𝑖);𝑖=1,2,3...
采用2-gram。于是有:
- 𝑃(𝑌1)=𝑃(“我司”,“可”,“办理”,“正规发票”) =𝑃(“我司”)𝑃(“可”|“我司”)𝑃(“办理”|“可”)𝑃(“正规发票”|“办理”)
- 𝑃(𝑌2)=𝑃(“我”,“司可办”,“理正规”,“发票”) =𝑃(“我”)𝑃(“司可办”|“我”)𝑃(“理正规”|“司可办”)𝑃(“发票”|“理正规”)
机器翻译与语音识别
N-gram语言模型在机器翻译和语音识别等顶级NLP应用中也有很大的用途。
用于判断生成的语句的后验概率相对大小。
平滑技术
拉普拉斯平滑
最简单的平滑技术是拉普拉斯平滑,
加一平滑法,其保证每个n-gram在训练语料中至少出现1次(或者加k)。
分母加上\(k * |V|\)
Back-off方法
考虑k-1元gram
插值法
多种gram加权
一元组 \((w_{i})\) 出现的次数平均比二元组 \((w_{i−1},w_{i})\) 出现的次数要多很多,根据大数定律,它的相对频度更接近概率分布。类似地,二元组平均出现的次数比三元组要高,二元组的相对频度比三元组更接近概率分布。
同时,低阶模型的零概率问题也比高阶模型轻。
\[P(w_i\mid w_{i-2},w_{i-1})=\lambda(w_{i-2},w_{i-1})\cdot f(w_i\mid w_{i-2},w_{i-1}) +\lambda(w_{i-1})\cdot f(w_i\mid w_{i-1})+\lambda f(w_i)\]
其中,三个 λ 为插值权重,均为正数且和为 1。
线性插值法的效果比卡茨退避法略差,故现在已经较少使用了。
古德-图灵
在统计中相信可靠的统计数据,而对不可信的统计数据打折扣的一种概率估计方法。
古德-图灵估计的原理是:
对于没看见的事件,我们不能认为它发生的概率就是零,因此我们从概率的总量(Probability Mass)中,分配一个很小的比例给这些没有看见的事件。这样一来,看见了的事件的概率总和就小于 1了。因此,需要将所有看见了的事件概率调小一点,并且按照“越是不可信的统计折扣越多”的方法进行。
假定在语料库中出现 r 次的词有 𝑁𝑟个,特别地,未出现的词数量为 𝑁0。语料库的大小为 N。那么,很显然:
\[N=\sum_{r=1}^{\infty}rN_r\]
出现 r 次的词在整个语料库中的相对频度(Relative Frequency)则是 \(r/N_r\)。
当 r 比较小时,它的统计可能不可靠,因此在计算那些出现 r 次的词的概率时,要使用一个更小一点的次数,是 \(d_r\)(而不直接使用r)。
\[d_r = (r+1)\cdot N_{r+1}/N_r\]
显然
\[\sum_rd_r\cdot N_r=N\]
根据 \(Zipf\) 定律,一般情况下 \(N_{r+1}<N_r\),因而 \(d_r<r\),从而 \(d_0>0\)。
\(Zipf\) 定律:一般来说,出现一次的词的数量比出现两次的多,出现两次的比出现三次的多,这种规律称为 Zipf定律(Zipf’s Law),即 r 越大,词的数量 \(N_r\) 越小。
这样就给未出现的词赋予了一个很小的非零值,从而解决了零概率的问题。同时下调了出现频率很低的词的概率。
实际运用中,一般只对出现次数低于某个阈值的词下调频率,然后把下调得到的频率总和给未出现的词。
于是:
- 对于频率超过一定阈值的词,它们的概率估计就是它们在语料库中的相对频度,
- 对于频率小于阈值的词,它们的概率估计就小于它们的相对频度,并且出现次数越少,折扣越多
- 对于未看见的词,也给与了一个比较小的概率
卡茨退避法(折扣)
由前 IBM 科学家卡茨(S.M.Katz)提出。
\(\sum_{w_{i-1},w_i\text{ seen}}P(w_i\mid w_{i-1})\lt 1\)类似古德-图灵估计的方法。这意味着有一部分概率量没有分配出去,留给了没有看到的二元组 \((w_{i−1},w_{i})\):
\[P(w_i\mid w_{i-1})=\begin{cases}f(w_i\mid w_{i-1})\quad\text{if }N(w_{i-1},w_i) \ge T \\f_{gt}(w_i\mid w_{i-1})\quad\text{if }0\lt N(w_{i-1},w_i)\lt T \\ Q(w_{i-1})\cdot f(w_i)\quad\text{otherwise}\end{cases}\]
其中 T 是阈值,一般在 8−10 左右,函数 \(f_{gt}()\) 表示经过古德-图灵估计后的相对频度。而
\[Q(w_{i-1})=\frac{1-\sum_{w_i \text{ seen}}P(w_i\mid w_{i-1})}{\sum_{w_i\text{ unseen}}f(w_i)}\]
类似地,对于三元模型,概率估计的公式如下:
\[P(w_i\mid w_{i-2},w_{i-1})=\begin{cases}f(w_i\mid w_{i-2},w_{i-1})\quad\text{if }N(w_{i-2,}w_{i-1},w_i) \ge T \\f_{gt}(w_i\mid w_{i-2,}w_{i-1})\quad\text{if }0\lt N(w_{i-2},w_{i-1},w_i)\lt T \\ Q(w_{i-2},w_{i-1})\cdot P(w_i\mid w_{i-1})\quad\text{otherwise}\end{cases}\]
Absolute discounting
Absolute discounting 包括了对高阶和低阶模型的差值,然而它并不是用高阶模型的 P 乘以一个 lambda,而是从每个非零计数里减掉一个固定的 discount δ∈[0,1],作为test set的计数。
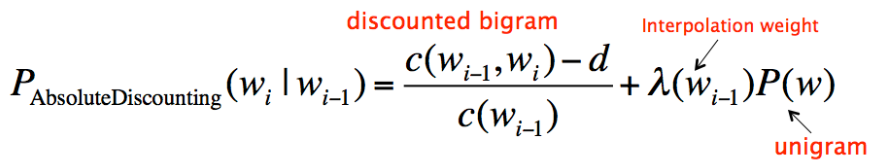
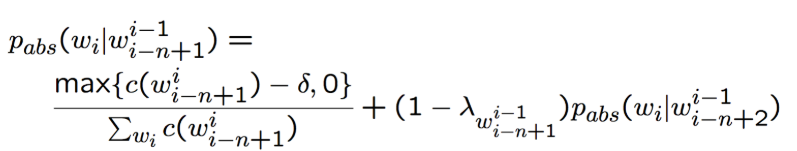
Kneser-Ney smoothing
Absolute discounting 的一个扩展,对回退部分做了一个修正。
只有在高阶模型的计数很小或者为 0 时,低阶模型才显得重要,(只有在 bigram 没有出现过时,unigram 才有用)。针对该目的进行优化。
目的: capture the diversity of contexts for the word。

Modified Kneser-Ney smoothing
根据高阶模型(k元)的相对大小,对低阶模型得到的部分进行比例分配。
目前在很多情况下,效果最好的平滑方法。
KenLM工具构建语言模型
https://kheafield.com/code/kenlm/
使用了Modified Kneser-Ney smoothing的语言模型工具包。安装和使用见notebook。
1 | |
神经语言预训练语言模型
BERT,GPT等,同样可以应用在以上领域。相关部分在后面笔记中给出。
参考资料:
Language Model: A Survey of the State-of-the-Art Technology
传统n-gram模型简单实用,但是数据的稀疏性和泛化能力有很大的问题。
当新的文本中出现意义相近但是没有在训练文本中出现的单词或者单词组的时候,传统离散模型无法正确计算这些训练样本中未出现的单词的应有概率,他们都会被赋予0概率预测值。
除了对未出现的单词本身进行预测非常困难之外,离散模型还依赖于固定单词组合,需要完全的模式匹配,否则也无法正确输出单词组出现的概率。
离散模型在计算上还存在“维度诅咒”的困难。假设我们的词库有一万个独立单词,对于一个包含4个单词的词组模式,潜在的单词组合多达\(10000^4\)。
神经网络模型:前馈神经网络模型(FFLM)和循环神经网络模型(RNNLM)。前者主要设计来解决稀疏性问题,而后者主要设计来解决泛化能力,尤其是对长上下文信息的处理。
前馈神经网络模型(FFLM)
Bengio等人提出的第一个前馈神经网络模型利用一个三层,包含一个嵌入层、一个全连接层、一个输出层,的全连接神经网络模型来估计给定n-1个上文的情况下,第n个单词出现的概率。其架构如下图所示:
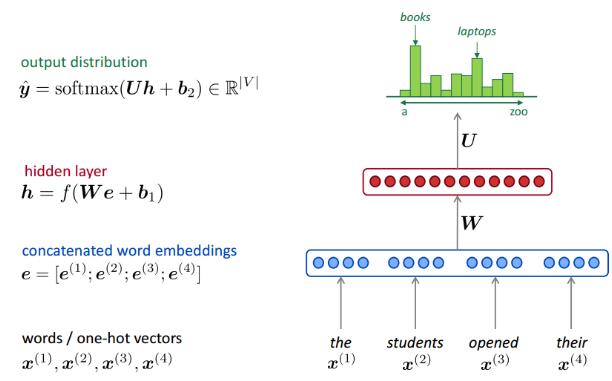
FFLM假设每个输入都是独立的。而循环神经网络的结构能利用文字的这种上下文序列关系。
循环神经网络模型(RNNLM)
循环神经网络模型不要求固定窗口的数据训练。
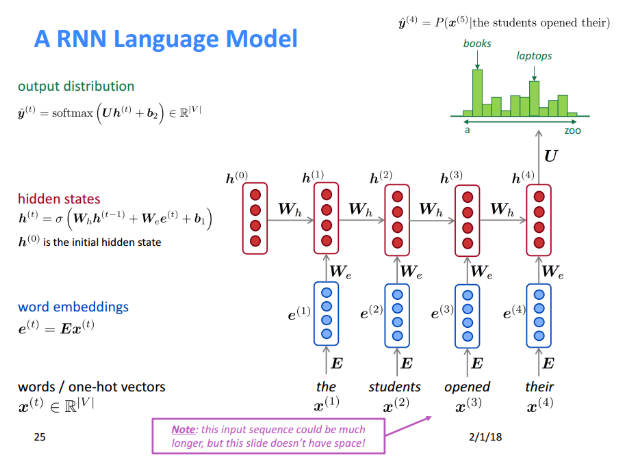
RNN语言模型训练过程:
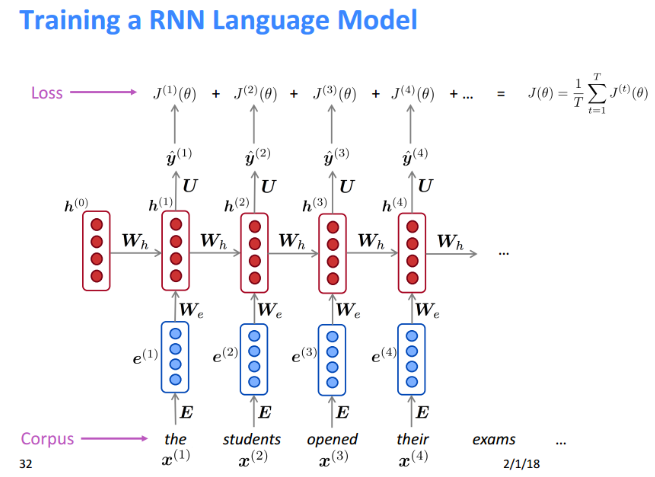
RNN语言模型反向传播:
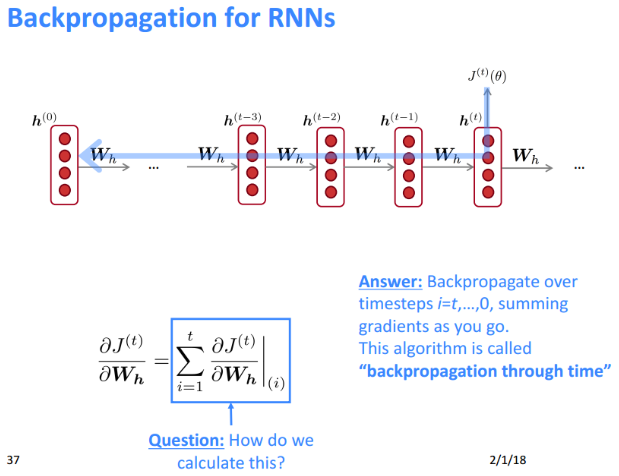
语言模型评估
困惑度(perplexity),其基本思想是给测试集的句子赋予较高概率值的语言模型较好。perplexity越小,句子概率越大,语言模型越好。
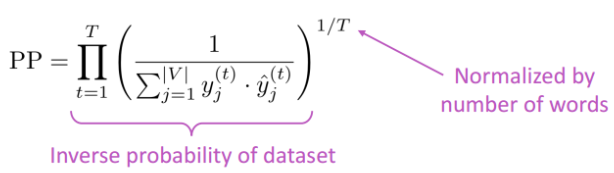
也就是,\(2^{-crossentropyloss}\)

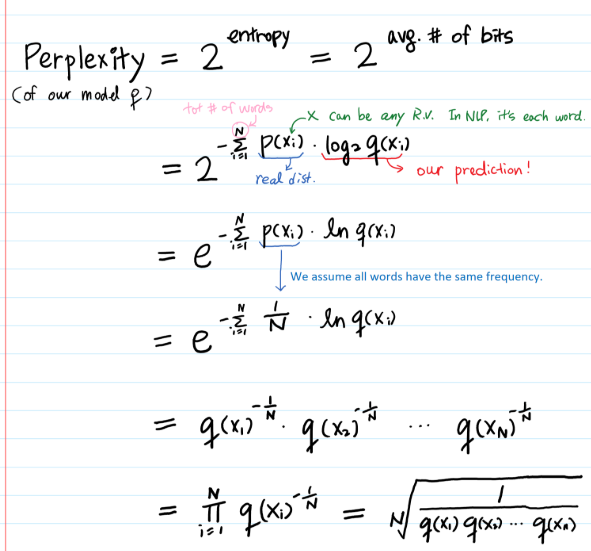
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!