C++编译器优化

x64寄存器模型

32 位 x86 架构中的通用寄存器有：eax, ecx, edx, ebx, esi, edi, esp, ebp

其中 esp 是堆栈指针寄存器，和函数的调用与返回相关。 eax 是用于保存返回值的寄存器。

64 位 x86 架构中的通用寄存器有：rax, rcx, rdx, rbx, rsi, rdi, rsp, rbp, r8, r9, r10, r11, ..., r15

其中 r8 到 r15 是 64 位 x86 新增的寄存器，给了汇编程序员更大的空间，降低了编译器处理寄存器翻车（register spill）的压力。

64 位比 32 位机器相比，除了内存突破 4GB 限制外，也有一定性能优势。

汇编语言

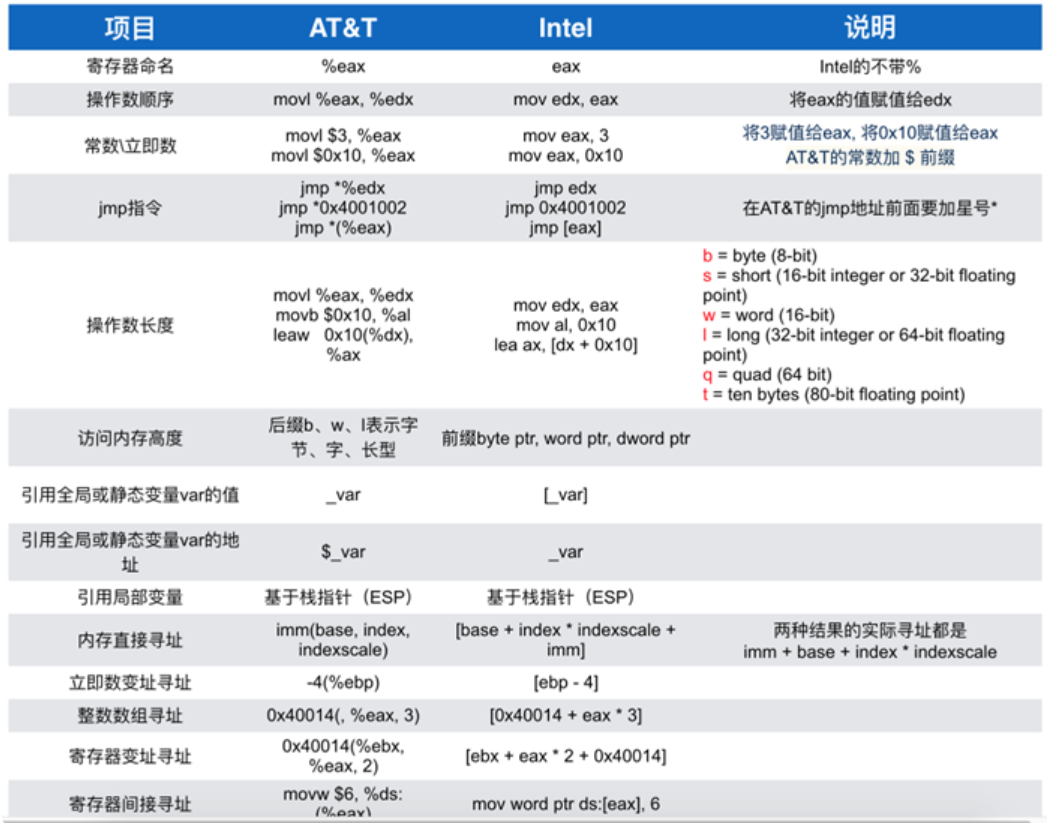
GCC 编译器所生成的汇编语言属于AT&T系列。

1	`gcc -fomit-frame-pointer -fverbose-asm -S main.cpp -o asm.S`

使用 -O3 （Release级别）查看编译器优化后的汇编程序。

1	`gcc -O3 -fomit-frame-pointer -fverbose-asm -S main.cpp -o asm.S`

lea

lea 是加载表达式的地址，相当于&。

1	`leal (%rdi,%rsi), %eax`

相当于

1	`eax = &*(rdi + rsi)`

线性地址访问优化

movslq 部分将32位寄存器扩展到64位，再进行访存计算。

优化建议：

指针的索引尽量用 size_t 类型。

不需要用 movslq 从 32 位符号扩展到 64 位，更高效。而且也能处理数组大小超过 INT_MAX 的情况。

推荐始终用 size_t 表示数组大小和索引。

浮点寄存器

浮点作为参数和返回使用 xmm 系列寄存器。

xmm 寄存器有 128 位宽。可以容纳 4 个 float，或 2 个 double。

对于浮点数寄存器操作指令，有特殊的指令形式。比如加法：

addss

add 表示执行加法操作。
第一个 s 表示标量(scalar)，只对 xmm 的最低位进行运算；也可以是 p 表示矢量(packed)，一次对 xmm 中所有位进行运算。（单个指令处理多个数据的技术称为 SIMD（single-instruction multiple-data））
第二个 s 表示单精度浮点数(single)，即 float 类型；也可以是 d 表示双精度浮点数(double)，即 double 类型。

即：

addss：一个 float 加法。 addsd：一个 double 加法。 addps：四个 float 加法。 addpd：两个 double 加法。

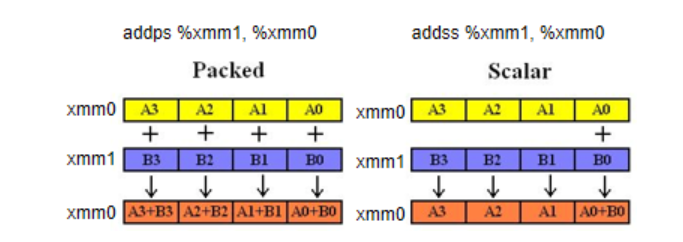
编译器生成的汇编里，有大量 ss 结尾的指令则说明矢量化失败；如果大多数都是 ps 结尾则说明矢量化成功。

SIMD

single-instruction multiple-data 可以大大增加计算密集型程序的吞吐量。

通常认为利用同时处理 4 个 float 的 SIMD 指令可以加速 4 倍。

但是如果你的算法不适合 SIMD，则可能加速达不到 4 倍；也可能因为 SIMD 让访问内存更有规律，节约了指令解码和指令缓存的压力等原因，出现加速超过 4 倍的情况。

编译器优化

对于简单的代数运算，编译器可以帮助优化计算，直接返回结果。

但是前提是：1. 代码简单；2. 代码不涉及动态内存分配。

代码过于复杂，涉及的语句数量过多时，编译器会放弃优化。

简单的代码，比什么优化手段都强。

堆上的容器

存储在堆上（妨碍优化）：

vector, map, set, string, function, any
unique_ptr, shared_ptr, weak_ptr

存储在栈上（利于优化）：

array, bitset, glm::vec, string_view
pair, tuple, optional, variant

constexpr

如果发现编译器放弃了自动优化，可以用 constexpr 函数迫使编译器进行常量折叠，但是会让编译变得很慢。

不过，constexpr 函数中无法使用非 constexpr 的容器：vector, map, set, string 等。

函数内联

如果函数的实现和声明分离，在调用时，被称为调用外部函数。调用时，链接器会通过 PLT 函数链接表，在其他 .o 文件中查找函数的定义。

如果函数实现就在调用的同一个文件中，称为内部函数。此时会直接调用，而不是通过链接器，减轻了链接器的负担。

只有定义在同一个文件的函数可以被内联。

为了效率我们可以尽量把常用函数定义在头文件里，然后声明为 static。这样调用他们的时候编译器看得到他们的函数体，从而有机会内联。

当编译器看得到被调用函数实现的时候，会直接把函数实现贴到调用他的函数里，实现函数内联。

inline 关键字

在现代编译器的高强度优化下，加不加 inline 无所谓。只要他看得见 other 的函数体定义，就会自动内联。

内联与否和 inline 没关系，内联与否只取决于是否在同文件，且函数体够小。

想要性能，定义在头文件声明为 static 即可，没必要加 inline 的。static 纯粹是为了避免多个 .cpp 引用同一个头文件造成冲突，并不是内联必需的。

可以实验测试，在线做编译器实验：https://godbolt.org/。

指针优化

void func(int *a, int *b, int *c) {
	*c = *a;
	*c = *b;
}

为什么编译器不优化掉 c = a？

因为 b 和 c 可能指向同一个变量。

优化前相当于：b = a; b = b; 最后 b 变成了 a。

如果优化了：b = b; 最后 b 没有改变。

这种情况叫做 pointer aliasing。

__restrict

__restrict 是一个提示性的关键字，是程序员向编译器保证：这些指针之间不会发生重叠（pointer aliasing），从而可以放心地优化。

实际上，__restrict 只需要加在所有具有写入访问的指针上，就可以优化成功。即只需加在非 const 参数之前即可。

因为只读的变量，随便几个指针指向它无所谓。

volatile

加了 volatile 的对象，编译器会放弃优化对他的读写操作。做性能实验的时候非常有用。

volatile 在 * 前面而，__restrict 在 * 后面。

volatile 是禁用优化，__restrict 是帮助优化。

restrict 是 C99 标准关键字，但不是 C++ 标准的关键字。__restrict 其实是编译器的“私货”，不在C++标准中，好在大多数主流编译器都支持。

矢量化

合并写入

编译器可以将两个 int32 的写入合并为一个 int64 的写入。但如果访问的两个元素地址间有跳跃，就不能合并了。

不管是编译器还是 CPU，都喜欢顺序的连续访问。

两个 int32 可以合并为一个 int64。四个 int32 可以合并为一个 __m128。

八个 int32 可以合并为一个 __m256。

xmm0 由 SSE 引入，是个 128 位寄存器。他可以一次存储 4 个 int，或 4 个 float。

如果硬件支持AVX指令集，还可以使用 256 位的 ymm0 寄存器。gcc -march=native 让编译器自动判断当前硬件支持的指令。

编译器会使用 SIMD 指令进行优化。

数组清零

编译器会自动分析你是在做拷贝或是清零，并优化成对标准库这俩的调用。

数组循环赋值

void func(int *a, int n) {
    for (int i = 0; i < n; ++i) {
        a[i] = i;
    }
}

n 如果是 4 的倍数，使用SIMD指令一次写入 4 个 int。

如果 n 不是 4 的倍数，将能被4整除的部分使用SIMD，剩余边界部分，每次处理 1 个。

如果能保证指针 a 总是对齐到 16 字节，在 GCC 编译器中这样写：

void func(int *a, int n) {
    n = n / 4 * 4;
    a = (int*)__builtin_assume_aligned(a, 16);
    for (int i = 0; i < n; ++i) {
        a[i] = i;
    }
}

C++20 引入了标准化的 std::assume_aligned

void func(int *a, int n) {
    n = n / 4 * 4;
    a = std::assume_aligned<16>(a);
    for (int i = 0; i < n; ++i) {
        a[i] = i;
    }
}

数组重叠

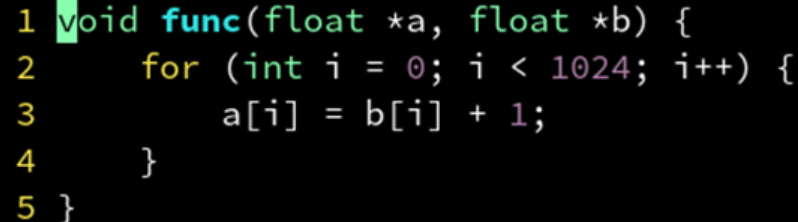
在运行时检测 a, b 指针的差是否超过 1024 来判断是否有重叠现象。

如果没有重叠，则跳转到 SIMD 版本高效运行。
如果重叠，则跳转到标量版本低效运行，但至少不会错。

编译器编译两个版本的代码，ps结尾指令为矢量化指令，ss结尾指令为标量化指令：

__restrict 关键字可以加以优化：

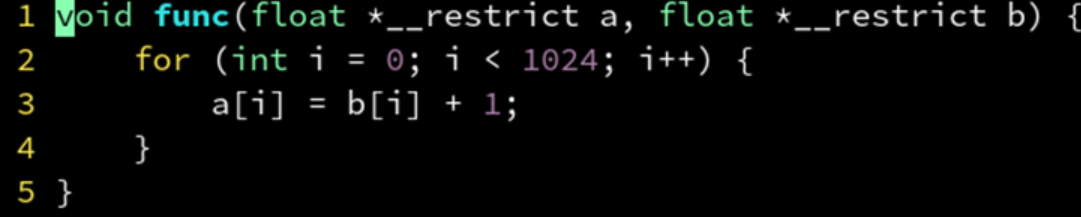
只需要生成一个 SIMD 版本了，没有了运行时判断重叠的焦虑。

或者，使用 OpenMP :

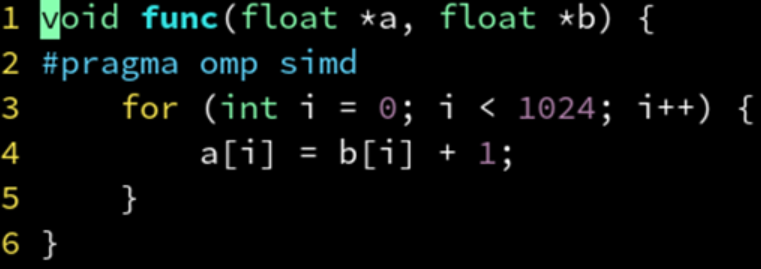
来迫使编译器无视指针别名的问题，并启用 SIMD 优化。编译参数设置为 gcc -fopenmp。

gcc 也提供了相似的编译指令：

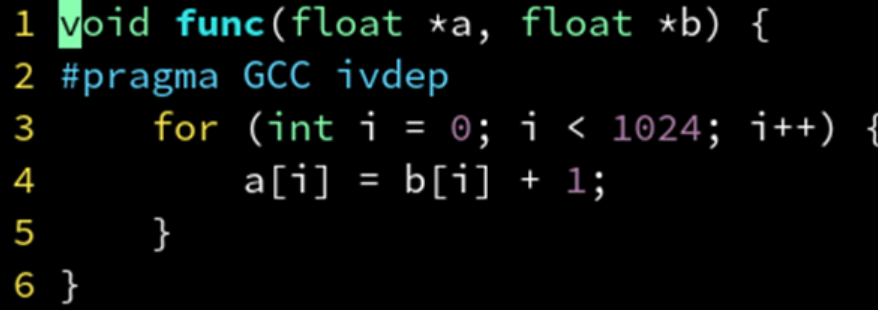
循环中的if

有 if 分支的循环体是难以 SIMD 矢量化的。

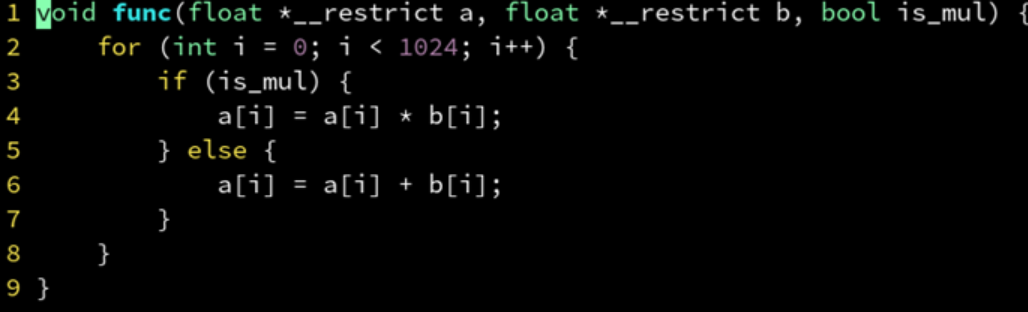
在编译器看来，is_mul 是一个常量，于是把 if 分支判断挪到了 for 外面来。

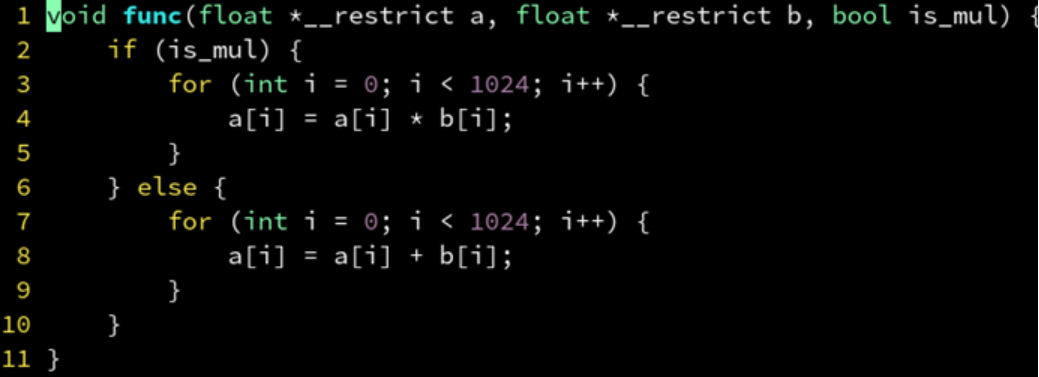
这样就可以使用 SIMD 指令。这一优化过程，编译器可以自动进行。

循环中的不变量

dt * dt 和当前 i 无关，因此可以移到循环体外，提前计算，避免重复计算。

在使用了（dt * dt）条件下，编译器可以自动优化，但是只要去掉 (dt * dt) 的括号就会优化失败。因为乘法是左结合的，就相当于 (b[i] * dt) * dt 编译器识别不到不变量，从而优化失败。

要么帮编译器打上括号帮助他识别，要么手动提取不变量到循环体外。

循环中的外部函数

避免在 for 循环体里调用外部函数，把他们移到同一个文件里，或者放在头文件声明为 static 函数。这样编译器能看到调用函数的函数体，才能进行内联优化。

循环展开

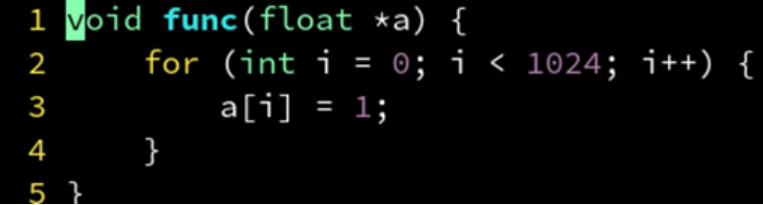
每次执行循环体 a[i] = 1后，都要进行一次判断 i < 1024。导致一部分时间花在判断是否结束循环，而不是循环体里。

对于 GCC 编译器，可以用 #pragma GCC unroll 4 表示把循环体展开为4个，相当于：

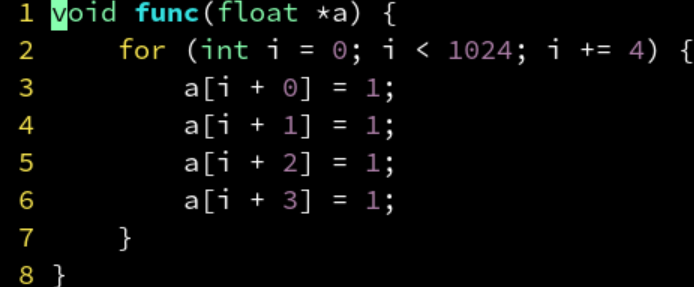
但是不建议手动这样写，会妨碍编译器的 SIMD 矢量化。

对小的循环体进行 unroll 可能是划算的，但最好不要 unroll 大的循环体，否则会造成指令缓存的压力反而变慢！

嵌套循环

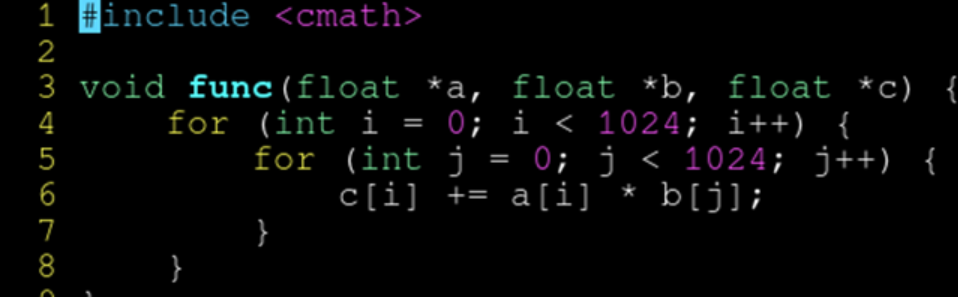
编译器担心 c 和 a 可能会指向同一个地址，而连续判断三个指针是否有重合又过于复杂，放弃了矢量化。

解决方案1：先读到局部变量，累加完毕后，再写入

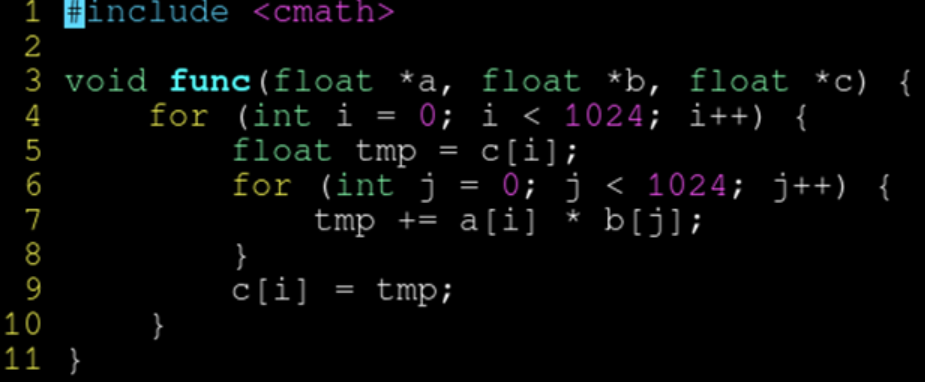
编译器认为不存在指针别名的问题，矢量化成功。

解决方案2：先累加到初始为 0 的局部变量，再累加到 c

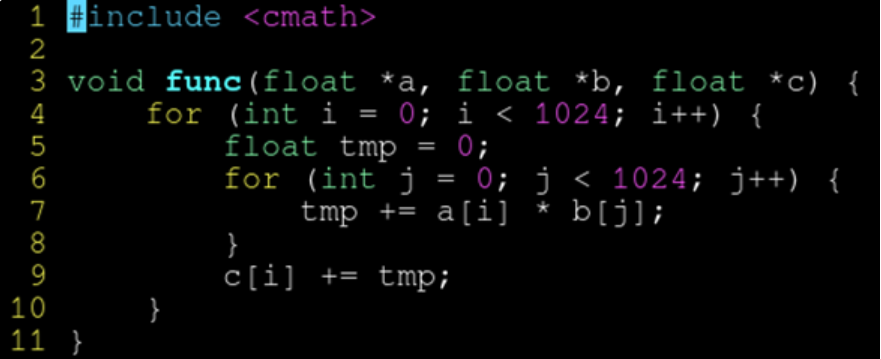
该解决方案比起前一种，由于加法顺序原因，算出来的浮点精度更高，c[i] 后面可能很大了。

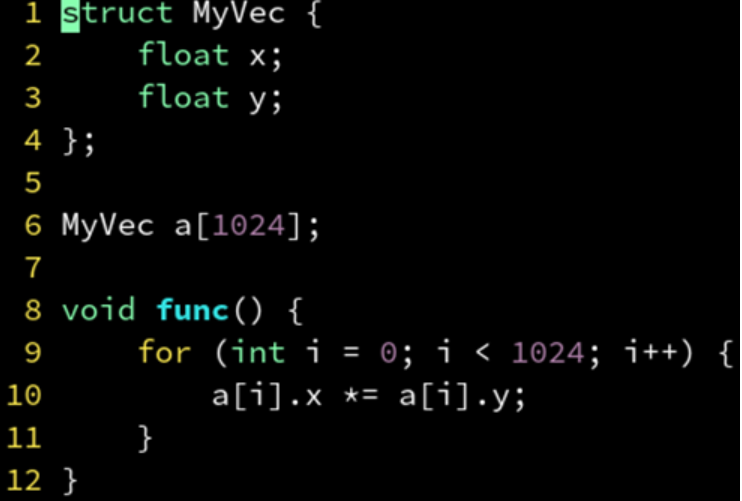
结构体

结构体对齐会影响到矢量化。

两个 float 的结构体，对齐到 8 字节，可以成功 SIMD 矢量化。

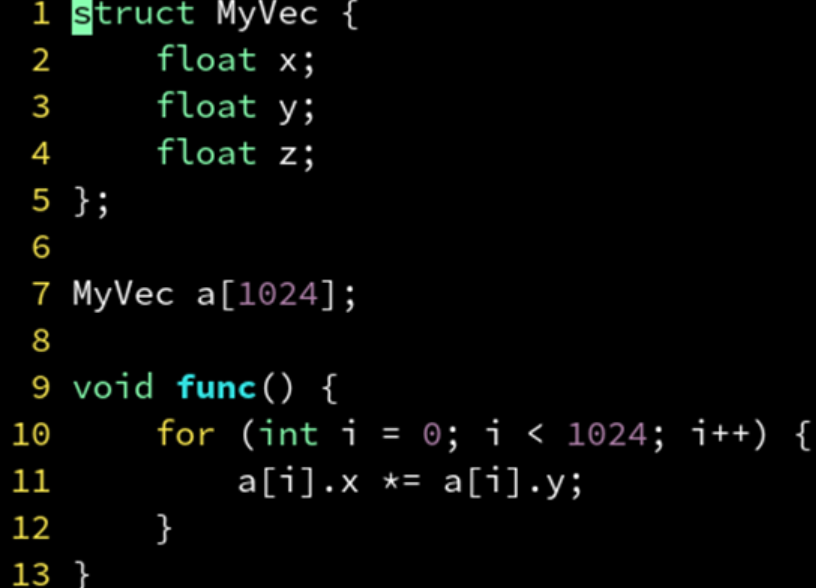
三个 float 的结构体，对齐到 12 字节，矢量化失败。

追加了一个没有用的 4 字节变量，整个结构体变成 16 字节大小。

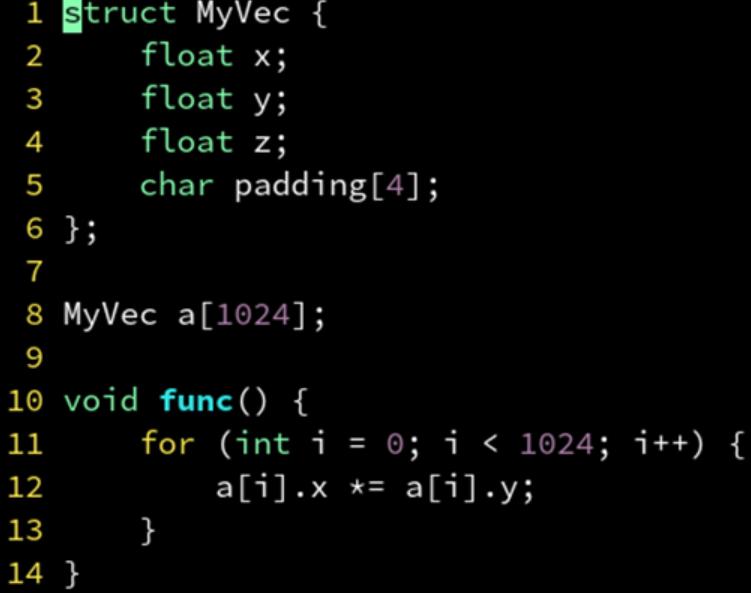
矢量化反而成功。

计算机喜欢 2 的整数幂，2, 4, 8, 16, 32, 64, 128...。结构体大小若不是 2 的整数幂，往往会导致 SIMD 优化失败。

alignas

C++11 的新语法。在 struct 后加上 alignas(要对齐到的字节数) 即可实现同样效果，就不需要手动写 padding 变量了。

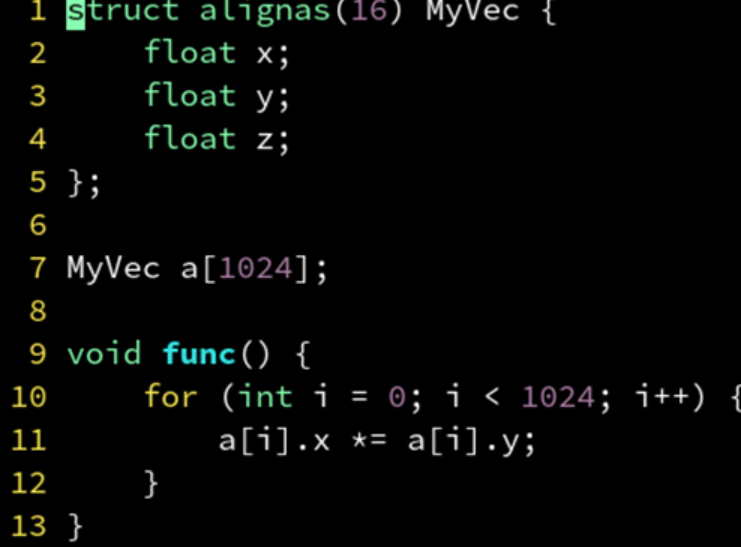
但是这种padding策略，也有可能不仅不变快，反而还变慢。SIMD 和缓存行对齐只是性能优化的一个点，又不是全部。还要考虑结构体变大会导致内存带宽的占用，对缓存的占用等一系列连锁反应，总之，要根据实际情况选择优化方案。

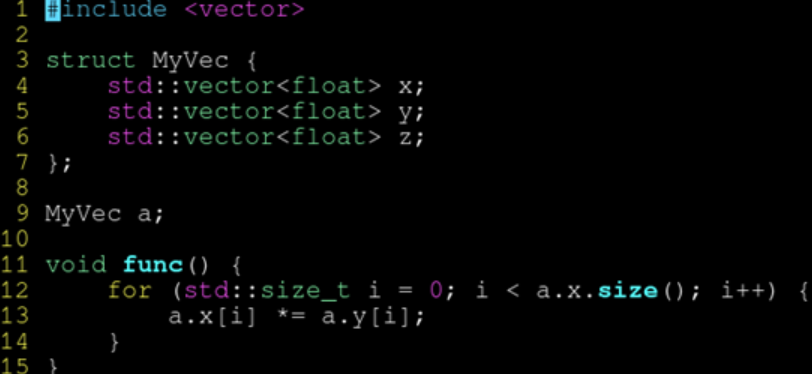
AOS 与 SOA

AOS（Array of Struct）单个对象的属性紧挨着存。SOA（Struct of Array）属性分离存储在多个数组。

AOS 必须对齐到 2 的幂才高效，SOA 就不需要。SOA 不符合直觉，但通常是更高效的。

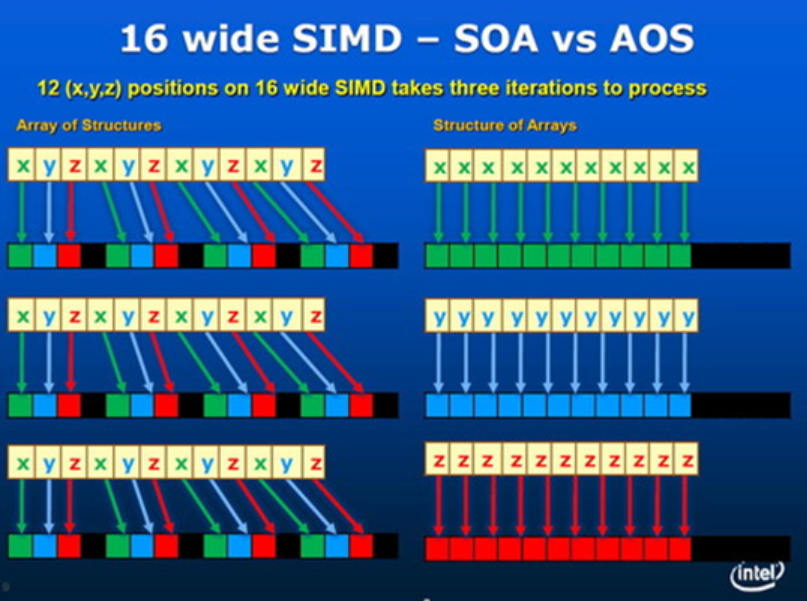
SOA：分离存储多个属性。不符合面向对象编程 (OOP) 的习惯，但常常有利于性能。又称之为面向数据编程 (DOP)。

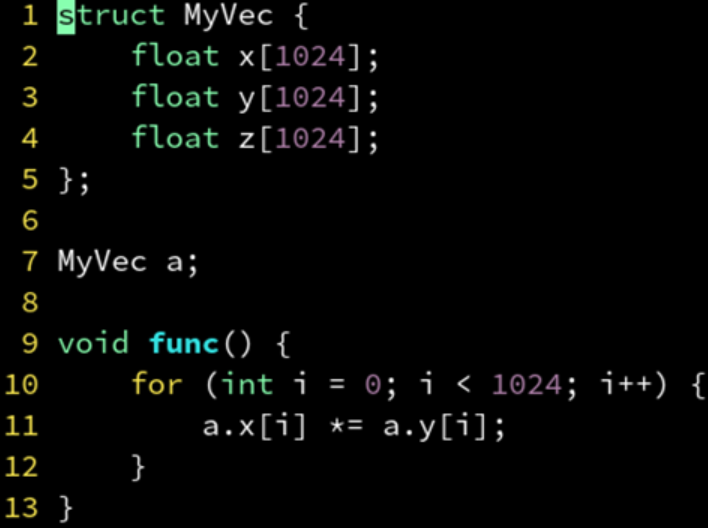
成功 SIMD 矢量化。

AOSOA

4 个对象一组打包成 SOA，再用一个 n / 4 大小的数组存储为 AOS。

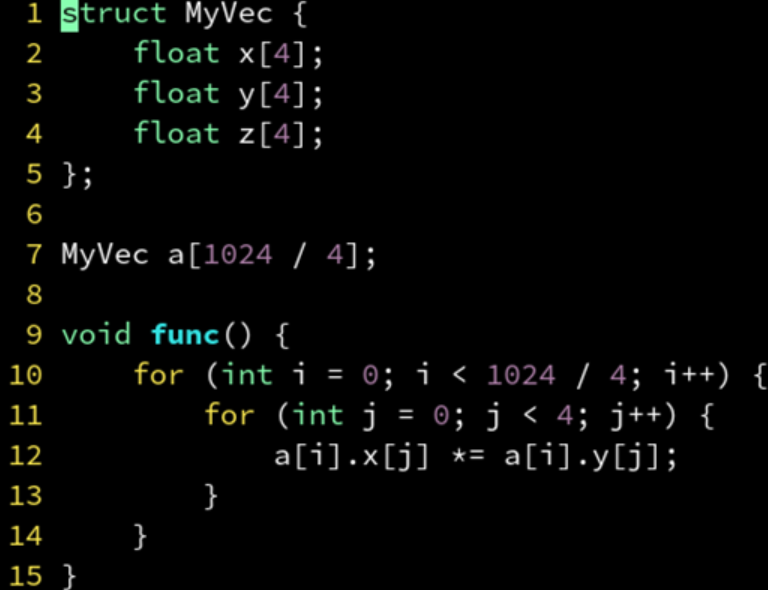
优点：SOA 便于 SIMD 优化；AOS 便于存储在传统容器；AOSOA 两者得兼。

缺点：需要两层 for 循环，不利于随机访问；需要数组大小是 4 的整数倍，不过可以用边界特判法（单独处理不能矢量化部分）解决。

Benchmark

aos

struct Point {
    float x;
    float y;
    float z;
};

Point ps[N];

void compute() {
    for (int i = 0; i < N; i++) {
        ps[i].x = ps[i].x + ps[i].y + ps[i].z;
    }
}

aos_aligned

struct Point {
    float x;
    float y;
    float z;
    char padding[4];
};

Point ps[N];

// 同compute

aos_parallel

struct Point {
    float x;
    float y;
    float z;
};

Point ps[N];

void compute() {
#pragma omp parallel for
    for (int i = 0; i < N; i++) {
        ps[i].x = ps[i].x + ps[i].y + ps[i].z;
    }
}

aosoa

struct Point {
    float x[M];
    float y[M];
    float z[M];
};

Point ps[N / M];

void compute() {
    for (int i = 0; i < N / M; i++) {
        for (int j = 0; j < M; j++) {
            ps[i].x[j] = ps[i].x[j] + ps[i].y[j] + ps[i].z[j];
        }
    }
}

soa

struct Point {
    float x[N];
    float y[N];
    float z[N];
};

Point ps;

void compute() {
    for (int i = 0; i < N; i++) {
        ps.x[i] = ps.x[i] + ps.y[i] + ps.z[i];
    }
}

soa_size_t

struct Point {
    float x[N];
    float y[N];
    float z[N];
};

Point ps;

void compute() {
    for (std::size_t i = 0; i < N; i++) {
        ps.x[i] = ps.x[i] + ps.y[i] + ps.z[i];
    }
}

soa_simd

struct Point {
    float x[N];
    float y[N];
    float z[N];
};

Point ps;

void compute() {
#pragma omp simd
    for (int i = 0; i < N; i++) {
        ps.x[i] = ps.x[i] + ps.y[i] + ps.z[i];
    }
}

soa_unroll

struct Point {
    float x[N];
    float y[N];
    float z[N];
};

Point ps;

void compute() {
#if defined(__GNUC__) || defined(__clang__)
#pragma GCC unroll 32
#elif defined(_MSC_VER)
#pragma unroll 32
#endif
    for (int i = 0; i < N; i++) {
        ps.x[i] = ps.x[i] + ps.y[i] + ps.z[i];
    }
}

soa_parallel

struct Point {
    float x[N];
    float y[N];
    float z[N];
};

Point ps;

void compute() {
#pragma omp parallel for
    for (int i = 0; i < N; i++) {
        ps.x[i] = ps.x[i] + ps.y[i] + ps.z[i];
    }
}

测试

#include <iostream>
#include <chrono>

template <class Name, class Func>
static inline void profile(int times, Name const &name, Func const &func) {
    auto t0 = std::chrono::steady_clock::now();
    for (int i = 0; i < times; i++) {
        func();
    }
    auto t1 = std::chrono::steady_clock::now();
    long dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t1 - t0).count() / times;
    std::cout << name << ": " << dt << std::endl;
}

结果

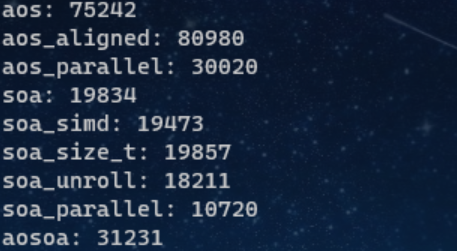
单线程的 SOA + unroll 甚至略微超过了并行版的 AOS。OpenMP 并非万能，单线程的程序认真优化后一样打败无脑并行。

性能还和array大小 N 有关。

std::vector

使用 pragma omp simd 或 pragma GCC ivdep 可以解决 vector 的 pointer aliasing 问题。

另外，使用 std::vector 也可以实现 SOA，不过，请保证 vector 是同样大小。

C++数学运算优化

除法变乘法

1
2
3

float func(float a) {
    return a / 2;
}

汇编变为mul乘法，* 0.5f。

但是以下程序却没有优化：

void func(float *a, float *b) {
    for (int i = 0; i < 1024; i++) {
        a[i] /= b;
    }
}

因为编译器害怕 b = 0。

乘法比除法更快，所以可以提前计算好 b 的倒数避免重复求除法。

void func(float *a, float *b) {
    float inv_b = 1 / b;
    for (int i = 0; i < 1024; i++) {
        a[i] *= inv_b;
    }
}

-ffast-math

-ffast-math 选项让 GCC 更大胆地尝试浮点运算的优化，有时能带来 2 倍左右的提升。作为代价，他对 NaN 和无穷大的处理。

如果你能保证，程序中永远不会出现 NaN 和无穷大，那么可以放心打开 -ffast-math。

数学函数请加 std:: 前缀

sqrt 只接受 double sqrtf 只接受 float std::sqrt 重载了 double 和 float（推荐）

abs 只接受 int fabs 只接受 double fabsf 只接受 float std::abs 重载了 int, double, float（推荐）

请勿用全局的数学函数，他们是 C 语言的遗产。始终用 std::sin, std::pow 等。

小结

函数尽量写在同一个文件内
避免在 for 循环内调用外部函数
非 const 指针加上 __restrict 修饰
试着用 SOA 取代 AOS
对齐到 16 或 64 字节
简单的代码，不要复杂化
试试看 #pragma omp simd
循环中不变的常量挪到外面来
对小循环体用 #pragma unroll
-ffast-math 和 -march=native

Notes C++

C++ Compiler

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

CMake Tips 上一篇

Unix用户终端登录过程分析下一篇