Embedding & Searching
相似性搜索常见于以图搜图,听歌识曲...这类抽象查找问题中。你没有明确的Key,不能使用SQL之类的方法查找数据库。但是可以通过抽象的 embedding 向量来进行检索。 一般样本向量表示可以通过 Skip-gram with negative sampling 方法、DSSM 这类方法、BERT 这类方法等等。得到向量表达之后,一般还需要高效的召回索引方法,因为暴力匹配在较大数据量场景下,速度通常差强人意。
这类通过抽象 embedding 的具有语义检索能力的方法,如下图所示:
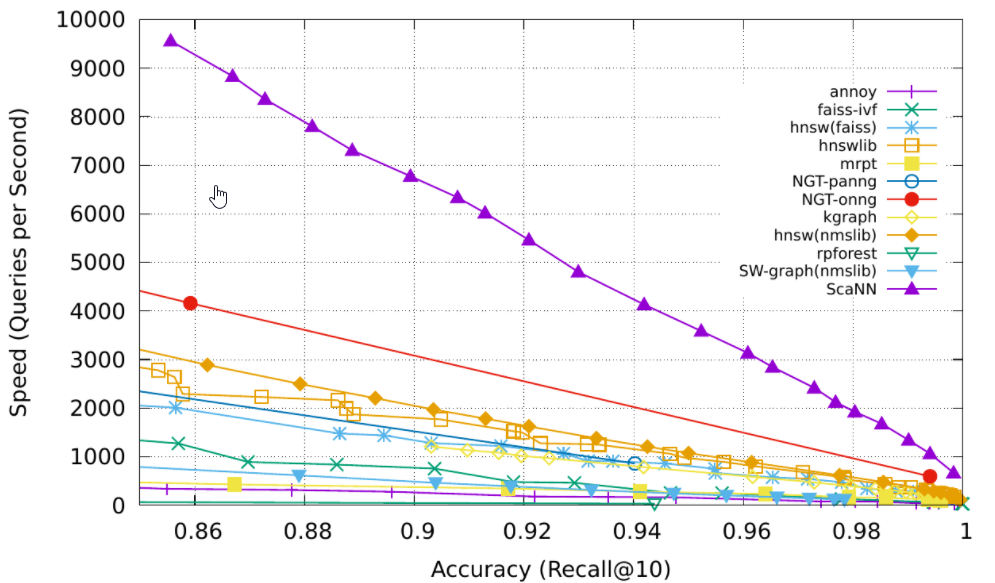
一组相关算法的 benchmarks 对比图如下:
Annoy
Spotify音乐公司开源的工具库。
这是一种基于树的方法。
算法简单描述:
定义: N -- 树模型的总个数;
K -- 叶节点最大样本数;
M -- 目标Top M样本数;
D -- 联通两个子空间所要求的最大距离;
过程:
==建树==
2
3
4for i in (1, ... , `N`):
1. 随机选取两个样本点,计算两者中点处超平面,划分两侧样本为两个子树;
2. 继续划分样本点,直到叶子节点中样本数不大于 `K`;
3. 保存二叉树(即保存每个划分点的值);==搜索==
2
3
4
5
6
7for j in (1, ... , `N`):
1. 从根节点开始,根据二分节点,向下遍历;
2. if 两个子空间相近(随机选的两个点距离小于 `D`),同时向两个子节点,向下遍历;
3. 保存找到的叶子节点空间(节点集合);
聚合`N`个叶子节点集合,以找到距离目标节点最近的 Top `M `个样本点;
返回结果
Annoy利用二叉树的结构对空间进行随机划分,建索引阶段效率有所提升。二叉树结构在检索时效率也很高。
特点:
- 召回率较优,和暴力搜索法相比较基本一致
- 查询速度很快
- 千万量级的item,时间为若干小时,尚可以忍受
- 千万量级的item,以100棵树为例,索引文件大约几个G,有点大了
- 多核利用支持的不是很好
ScaNN
ScaNN是google提出的高效向量检索算法,文中说这个方法比目前已有的其他方法有更高的精度,检索速度也要快两倍。工具库开源地址 GitHub。
这种算法主要是优化 Inner product 距离度量下的搜索。这类问题被叫做 maximum inner-product search (MIPS)。在大数据量场景下,MIPS的计算复杂度是比较高的,穷举搜索几乎不可能在期望的时间范围内完成。
论文中,阐述了目前使用的向量压缩(比如聚类或者降维)所使用方法,会使得压缩后的向量间平均距离变小。这可能导致了向量差异性的损失,比如与query向量的内积的相对大小关系会出现错误。比如这样:
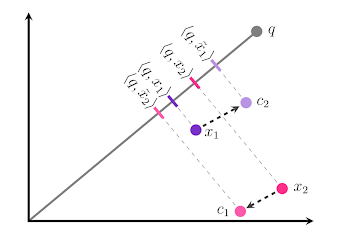
上图中,x 被分别压缩到 c 点,其余 q 的内积大小关系发生颠倒。本来 \(<q,x_2> greater\ than <q,x_1>\), 压缩后 \(<q,x_1> greater\ than <q,x_2>\)。
论文中指出,这种方法压缩,只考虑了距离的长度大小,而没有考虑距离的角度方向。
一个简单的例子,计算两个向量的内积,当一个向量在平行于投影方向(两个向量方向都可作为投影方向)变化 k ,内积的变化为 \(d_1\)。而如果实在一个向量的垂直方向,变化 k ,内积的变化为 \(d_2\)。那么,\(d_2 ≥ d_1\)一定成立。画个图就能验证。
所以,现在在压缩时,对于 x 与 c 在平行于 x 向量方向上的变化,给予一个大的惩罚项;而对于 x 与 c 在垂直于 x 向量方向上的变化,给予一个较小的惩罚项。以此来进行压缩。取了名字叫,Anisotropic Vector Quantization。
效果如下:
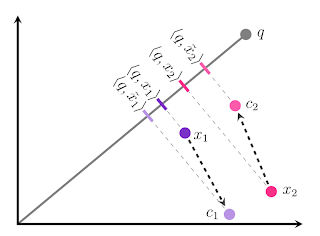
内积相对大小关系,没有变化。按照论文中的说法,这样做最大化了压缩后各个点之间的平均距离,有利于差异化相似度的值。
算法大致流程:
- 根据样本数量大小,选择是否将数据进行 Partitioning。若 Partitioning,在检索时,会先选出 Top m 个Partitioning,再进行细化检索。
- Scoring:使用快速的粗粒度的距离度量,计算query相对所有样本(或Partition的样本)的距离。选出 Top k 个。
- Rescoring: 对 Top k 个Scoring结果,进行更精确的距离度量,重拍后输出 Top k 的结果。
使用 doc 比较简短,可以参考。
HNSW
HNSW是一种图算法。其根据搜索场景的特点,设计出了这种算法。
首先,简单想想图的搜索,麻烦的问题可能有哪些。可能有孤立的节点,或者可能相邻节点太多。在近邻搜索场景下,可能有几个距离目标很近的节点,但是没有相互连通,那么就需要遍历更多的路径,从而遍历完全这几个节点。
另外,节点众多时,当两个节点距离相对较远时,遍历数量会指数级增加。
HNSW的解决方法如下:
定义:
N -- 总样本数;
K -- 每个节点最多有K个相连的近邻节点;
P1 -- 以 P1 的概率将节点设置为二级索引;
P2 -- 以 P2 的概率将节点设置为一级索引(P1 > P2,两者指数递减);
M -- 目标Top M样本数;
过程:
==建图==
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20for i in (1, ... , N):
if (随机概率值 p) > P1:
二级索引图插入节点:
1. 将被插入节点连接指向最近邻的 K 个节点(小于等于 K);
2. 更新被连接的 K 个节点(小于等于 K)的最近邻的 K 个节点;
3. 保证每个节点都有连接,且最大连接不超过 K;
if (随机概率值 p) > P2:
一级索引图插入节点:
1. 将被插入节点连接指向最近邻的 K 个节点(小于等于 K);
2. 更新被连接的 K 个节点(小于等于 K)的最近邻的 K 个节点;
3. 保证每个节点都有连接,且最大连接不超过 K;
全量样本索引图插入节点:
1. 将被插入节点连接指向最近邻的 K 个节点(小于等于 K);
2. 更新被连接的 K 个节点(小于等于 K)的最近邻的 K 个节点;
3. 保证每个节点都有连接,且最大连接不超过 K;
返回建立的多级索引图==搜索==
2
31. 在二级索引图中找到最近邻节点 A
2. 在一级索引图中从 A 开始找到最近邻节点 B
3. 在全量样本索引图中从 B 开始找到 Top M 的目标节点
HNSW设计的插入机制,保证了图具有良好的连通性和局部搜索便捷性。类似跳表结构的多级索引机制,提高了搜索效率,降低了整体搜索复杂度。
算法细节看文章,这里只是草草写写思想。开源工具库C++版:hnswlib
特点:
- 召回率优秀,和暴力搜索基本一致
- 千万量级的item,构图可在分钟级别完成
- 多核利用优秀
- 查询速度很快
LSH
在 min hash 之上,更进一步优化了在大量文本相似性聚类的算法。首先需要计算每一个文本的多个不同 min hash 表示,构成 min hash 值向量。然后对 min hash 向量分块进行简单的元素对比,检查是否相似。此处LSH,只关注基于 Jaccard similarity 的文本处理,其他LSH实现不涉及。
这就是一种基于词统计的 hash 分桶算法。其中没有计算欧式距离这种计算量较大的操作,仅仅是元素对比。
算法如下:
定义: K -- 取文本中连续 K 个词为bag of words的计数对象(这里被称为 K-Shingling);
N -- min hash向量的维度,即进行随机 min hash 的次数;
M -- 文本总数;
b -- LSH中hash分组的组数;
r -- b组 min hash 子向量的维度;
过程:
==min hash==
2
3
4
5
61. 对整个文本集构建以 K 个连续词为一个对象的bag of words统计矩阵,文本中存在的对象标记为1,不存在标记为0;
2. for i in (1, ... , N):
A. 随机指定统计矩阵中一个 index 为起始位置(保存index);
B. 从 index 开始,在每一个文档列中,向下查找第一非 0 位置;
C. 取第一非 0 位置与 index 位置的偏移量为 min hash 向量的第 i 行,有 M 个 min hash 向量;
3. 得到 (N, M) 的 min hash 矩阵==局部敏感hash(LSH)==
2
3
4
5
61. 将 min hash 矩阵均分为 b 组;
2. 分桶聚类:
for j in (1, ..., b):
A. 两两对比第 j 组 min hash 子向量;
B. 子向量完全相同时,将该两个向量对应文本,放到一个相似桶中(类似聚类);
3. 保存分桶结果,每个桶中就是相似的文本
关于 min hash,它就是一种 Jaccrad similarity 的另一种表示。
\(P(hash(S_i)=hash(S_j))\) 就等价于 \(Jaccard(S_i, S_j)\)。证明也挺简单的:
只看两个 min hash 向量中不全为 0 的行,记为 \(sub\_hash\)。
此时 \(hash(S_i)=hash(S_j)\) 概率就等价于 \(sub\_hash\) 的第一行都为 1 的概率。
\(sub\_hash\) 的第一行都为 1 的概率,就等于\(sub\_hash\) 中{两列都为 1 的行数 / 任意一列为 1 的行数}。
\(sub\_hash\) 中{两列都为 1 的行数 / 任意一列为 1 的行数},就是 \(Jaccard(S_i, S_j)\)。
另外,调整参数 b 和 r
可以间接调整分桶的相似性阈值。假设两个 min hash 向量相似概率为 \(p\)。分到同一个桶中的概率可表示为(只要有一组
sub hash 相同就分到一个桶): \[
1 - (1 - p^r)^b
\] 开源工具库:mattilyra/LSH
特点:
- 查找速度快
- 方便去重处理
- 处理大量数据速度较快
Product Quantizer
Product Quantizer简称为PQ,是一种建立索引的方法。优化了K-Means聚类的计算量。
定义:
N -- 样本总量; D -- embedding维度; K -- 子空间数量; C -- K-means聚类类别数;
过程:
==建索引==
2
3
4
5
6
7
81. 将 N 个 D 维embedding,切分为 K 组 (N, D/K) 的embedding;
2. for i in (1, ..., K):
A. 对第 i 个 (N, D/K)的embedding,计算 C 个聚类中心点
3. for j in (1, ..., N):
for k in (1, ..., K):
A. 将第 j 个样本标记到第 k 组聚类的所属中心点编号;
B. 循环得到第 j 个样本的 K 维中心点编号向量;
得到 (N, K) 的样本编码矩阵==搜索==
2
3
4
5
6
7
8
9
10
11
12
13
14
15
161. 将输入 embedding 划分为 K 组 sub embedding;
2. for i in (1, ..., K):
for j in (1, ..., C):
A. 计算 sub embedding 与聚类中心 j 的距离;
B. 循环得到 C 维的距离向量;
循环得到 (K, C) 的距离矩阵
3. 计算输入与所有样本的距离:
for i in (1, ..., N):
取 (N, K) 的样本编码矩阵中第 i 行 (1, K), 记为 Q;
定义输入与样本 i 的距离为 di;
for k in (1, ..., K):
A. 取 Q[k] 的值,记为 q;
B. 取 (K, C) 的距离矩阵中第 k 行,记为 dist;
C. di += dist[q];
记录输入与样本 i 的距离为 di 的值;
4. 从 N 个 di 距离中找到需要的样本
这种方法,将暴力搜索,转化为 K * N 次距离表查找过程。
Inverted File System
这个方法(简称 IVF)相当于使用倒排表来优化索引。比如 IVF + PQ,来优化 K * N 次的查询操作。IVF, PQ 在 Faiss 库中都有实现。
简述一下方法:
在 PQ 建立索引的过程中增加一步:
将 (N, K) 的样本,分别保存到
C_ivf个聚类之下,即,保存到C_ivf个代表一个类的数组中。得到C_ivf个类别字典,key 为聚类中心点(id),value 为该聚类中所有样本点的 PQ 编码数组。(按照C_ivf个聚类类别进行倒排样本)
在 PQ 查询中增加一步:
在第三步第二层 for 循环中,先求得与输入样本最近的
C_ivf聚类中心,然后在该聚类的 PQ 编码数组中计算每个样本与输入的距离。
利用倒排,减少了搜索范围。从全部样本搜索,变成先找聚类,再在类中搜索。
这里建立倒排的 K-means 聚类与 PQ 中使用的不同,使用一个更粗粒度的 K-means 聚类,但是没有对 N 个 embedding 进行划分。
显然,IVF虽然建立索引的过程更复杂一些,但是搜索的过程会更快速。
Structure-based Approximations
这类近似搜索,将搜索过程抽象为一个神经网络表示的函数,输入对象,输出搜索结果。当然以下方法需要监督数据支持,或者可以构建无监督的共现关系。
Negative sampling softmax:
简化版的NCE近似计算,将多分类,转为多个正负例二分类。复杂的负例分布抽样时,可以采用importance sampling进行简化。
Class-based softmax:
使用两个softmax,第一个预测 class,第二个基于输入和 class 预测搜索目标。
Hierarchical softmax:
构建 Huffman tree,然后每个节点只进行一个二值分类预测,直到叶子节点。预测直接变成了 tree height 次二分类计算。
Binary code prediction:
将所有对象的index,转化为二进制表示,使用多个sigmoid,预测每个位置是 0 还是 1,得到目标index的二进制表示。
Embedding Prediction:
预测 embedding 表示。这个方法是对 Embedding inference 模型的近似,思路基本上和蒸馏差不多。对于下游搜索匹配,没有影响。这个方法用到一种损失,Von-Mises Fisher distribution loss,约束了输出embedding靠近一个单位球面(超球面)。
End
相似性搜索,和计算 margin loss 的分类问题目标比较接近。 \[ Loss_{margin}(x,y,\hat{y})=max(0, 1+s(\hat{y}|x)-s(y|x)) \] 另外,基于树的搜索,还有KD Tree算法,这里不涉及。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!