BERT-flow and more

论文: On the Sentence Embeddings from Pre-trained Language Models

Author: Bohan Li, Hao Zhou, Junxian He, Mingxuan Wang, Yiming Yang, Lei Li

Organization: ByteDance AI Lab; Language Technologies Institute, Carnegie Mellon University

Info:

  • 类别: BERT语义表示应用优化

  • 研究目标：将原本BERT训练模式下生成的语义表示的各向异性空间，通过设计的无监督方法，转化为各向同性的语义表示空间。

  • 研究成果：结合Flow based model，使用无监督方式提升语义表示的效果。

  • 存在的问题：按文章的思路，就是将BERT sentence embedding做一个转化，从非正交（orthogonal space）转化到正交的空间，以满足cos similarity适用的条件，以提高效果。但是一定需要Flow based 方法来实现吗？有没有更好的方法？

  • 关键词：BERT；Flow based model；semantic similarity

Brief Summary:

首先解释了直接基于BERT生成的sentence embedding为什么其语义表达能力较差，然后提出一种在不引入更多监督数据条件下，提升其语义表达能力的方法，flow based model。

Outline:

  1. 搞清楚BERT-induced sentence embedding的空间有什么特性
  2. BERT-flow怎么设计的
  3. [来自苏剑林的质疑] BERT-flow？没必要那么复杂，BERT-whitening更优雅

Main Thought:

首先是flow based model在干什么，这首先是一个生成网络（以下图片内容来自李宏毅老师课程）：

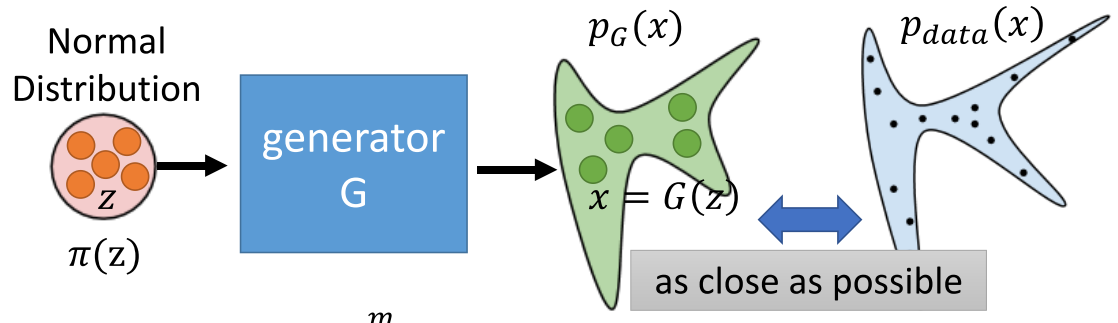
这是一种直接在object function基础之上优化计算的方法，粗暴但是实现起来并不简单。直接从\(\pi(z)\)，由设计的网络\(x=f(z)\)，直接逼近data分布\(p(x)\)。原理如下：

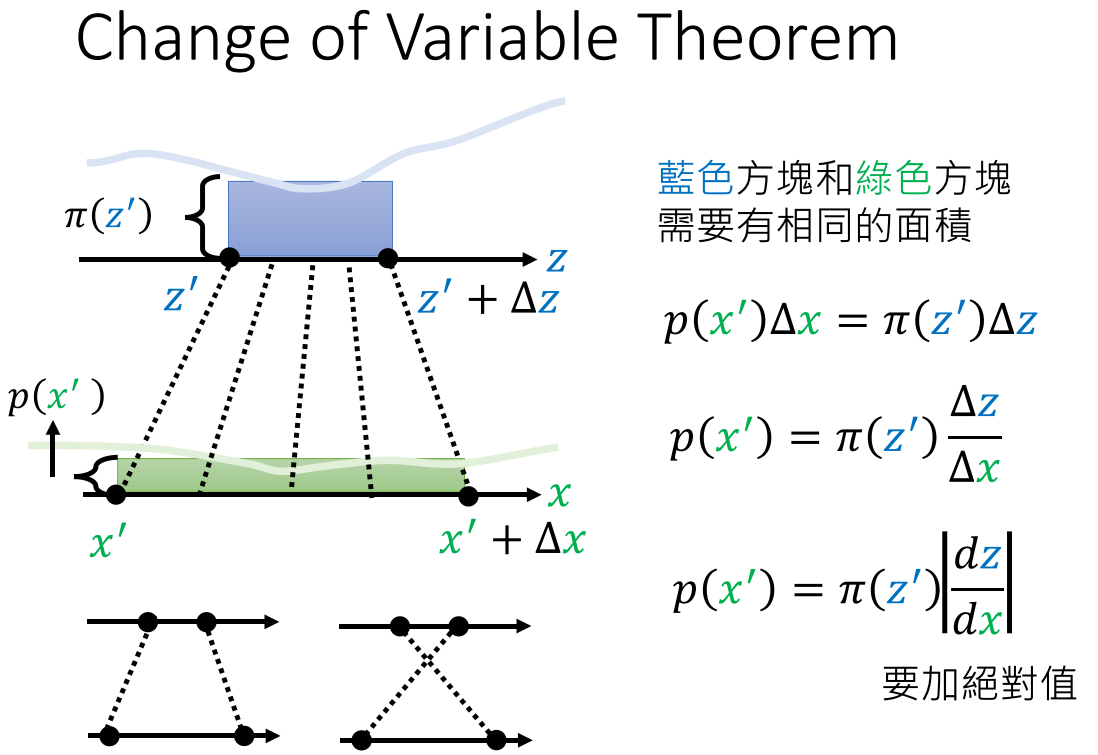
相应变量的微小变化，导致的面积变化是一致的。扩展到二维变量，其变化相乘变成了面积的\(\Delta s\)。而矩阵的行列式就表示二维空间中图像代表的面积，所以有以下推导：

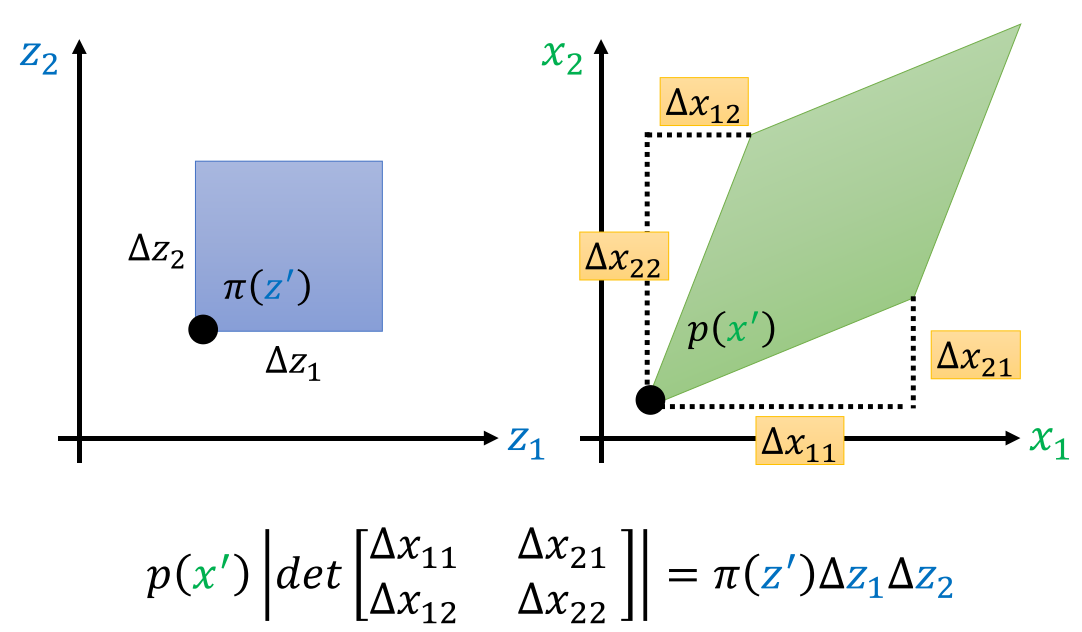
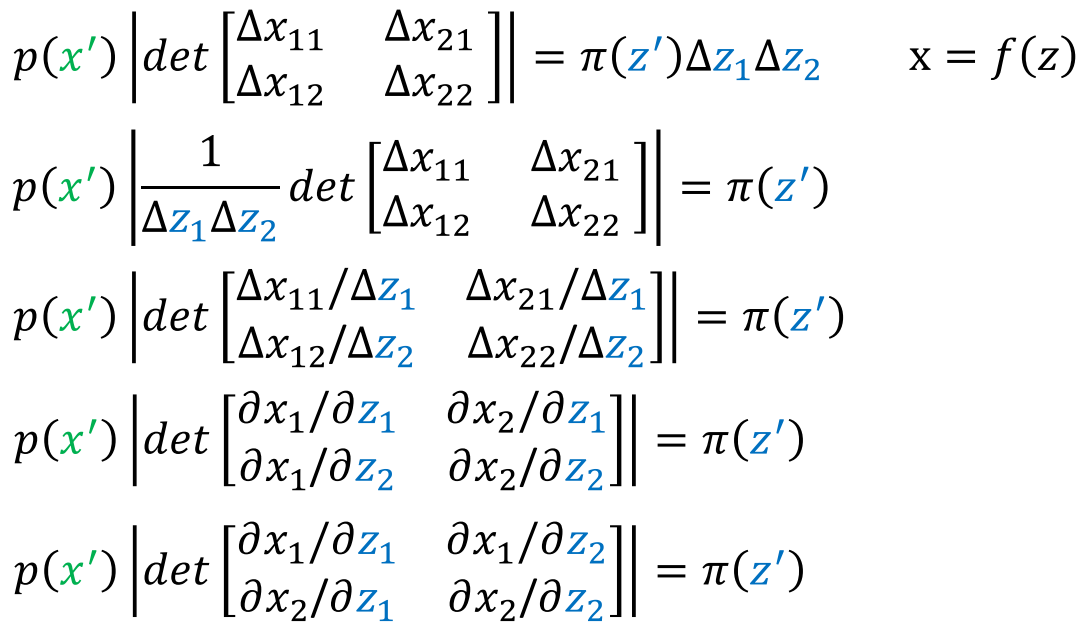
式中矩阵就是Jacobian matrix，自然得到： \(p(x')=\pi(z')|\frac{1}{det(J_f)}|\) 那么由\(z\)的分布就可以求出\(x\)的分布。只是这个网络\(G\)的设计有一点麻烦，需要保证参数矩阵需要是逆变换不复杂且Jacobian matrix容易计算。因为： \(p(x')=\pi(z')|det(J_{G^{-1}})|\) 以及 \(z'=G^{-1}(x')\)

都需要转化成与输入相关的函数（网络）。

同时flow的网络设计，真的是有点低效，参数空间内将参数分组进行更新。

如图，上下两部分不是同时更新，而是分步更新计算。

Key sentences:

  1. 用BERT将一个句子编码成一个固定长度的向量，方法是计算BERT最后几层中context embeddings的平均值，或者在[CLS]标记的位置提取。一般前一种方法效果更好。但是在语义表示性能上还不及averaged GloVe embeddings方法。

1. 语义相似度与BERT预训练的关系

​ 首先，BERT将传统的auto regressive LM的目标，修改为masked predict： \[ log(p(x_{1:T}))=\sum_{t=1}^{T}logp(x_t|context_t) \] 变为： \[ p(x_{masked}|context_{of\ masked})=\sum_{t=1}^{T}mask_t \times p(x_t|context_t) \] 两者建立model的共同形式如下： \[ p(x|context)=\frac{\exp(VectorFromNet_{context}^TEmbedding_x)}{\sum_{x'}\exp(VectorFromNet_{context}^TEmbedding_{x'})} \] 这种表达形式的关键在\(VectorFromNet_{context}^TEmbedding_x\)，以下简单写作\(h_c^Tw_x\)。这篇论文证明了： \[ h_c^Tw_x\approx\log p^*(x|c) + \lambda_c=PMI(x,c)+\log p(x)+\lambda_c \] ​ PMI指point wise mutual information。这种共现特征通常可以捕捉到语义信息，只是在“word”层面而言。

​ 同时，\(h_c\)随着网路参数的更新而更新，不同的context在训练过程中相互影响，可视为一种高阶的high-order共现语义信息捕捉。

2. 问题所在

用BERT将一个句子编码成一个固定长度的向量，方法是计算BERT最后几层中context embeddings的平均值，或者在[CLS]标记的位置提取。一般前一种方法效果更好。但是在语义表示性能上还不及averaged GloVe embeddings方法。

为什么效果不及averaged GloVe embeddings？

文章 How Contextual are Contextualized Word Representations? Comparing the Geometry of BERT, ELMo, and GPT-2 Embeddings 比较了预训练LM的word embedding，有如下结论：

  1. Contextualized representations(模型每一层输出)在每一个非输入层都是各向异性的，即非标准正交空间；
  2. 高层的各向异性更显著；
  3. 高层的Contextualized representations更与context相关，不同context下的数值表示相差更大。同时不同词与context相关的相关程度不同，比如，stop words与context的相关性会很大；
  4. 不同模型的每一层输出间的相关性也不同：EMLo的低层和高层的输出更相似一些；BERT的低层和高层的输出变化较大，同时句子内词的表示会更接近，和其他句子中词的表示相对更差异化一些；GPT-2的输出不同，某一个输出与当前句子内的词的相似性和当前句子之外的词的相似性，是接近的。

BERT-flow文中给出的理由：

  1. 词频差异使得低频词和高频词的学习程度不同，公式7可以作为一个依据；
  2. 低频词的表示更偏稀疏，而高频词的表示更稠密。

3. 可逆变换到standard Gaussian latent space

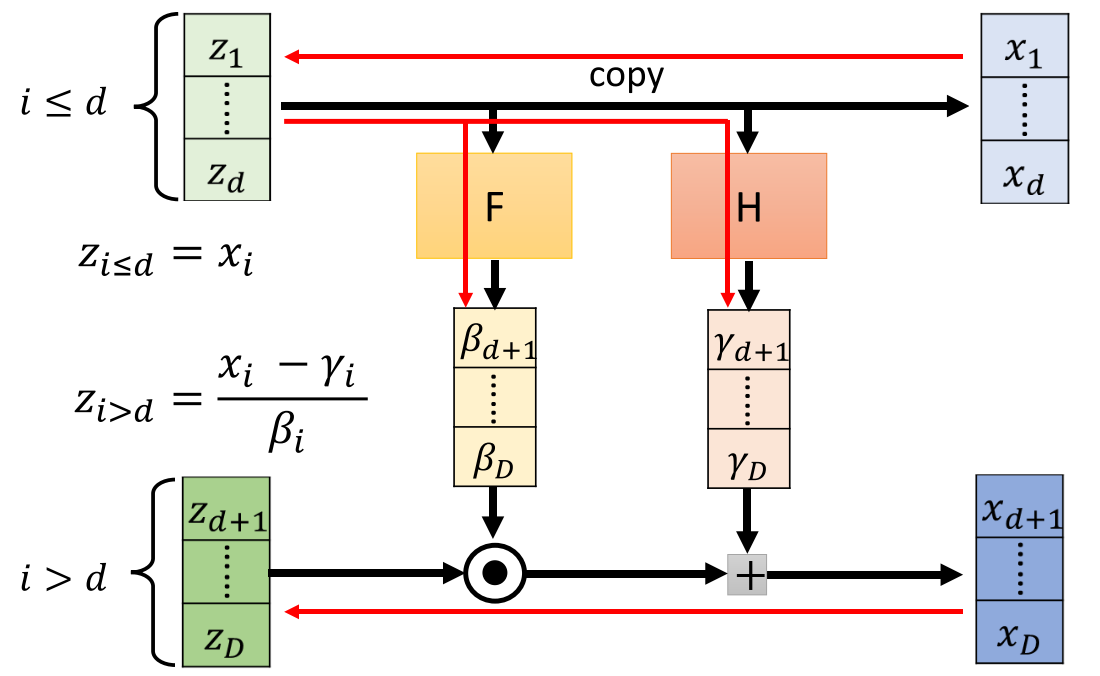
借鉴Glow模型的实现方式，实现flow-based generative model。将BERT参数固定，只学习可逆变换的网络参数。只使用了add coupling layer，将1x1卷积变成直接permutation。

求z为：

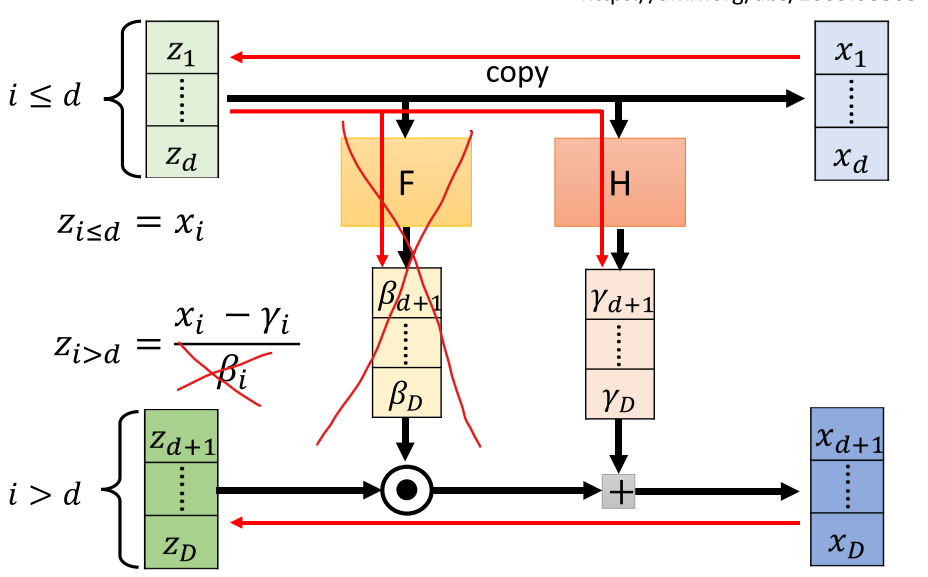
以上将D维向量，分为两部分计算更新。同时z的先验为标准正态分布。那么

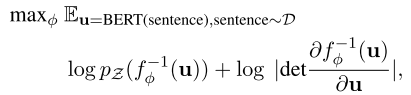
\(f^{-1}\)和\(J_{f^{-1}}\)都是可以计算的，目标函数就可以表示。

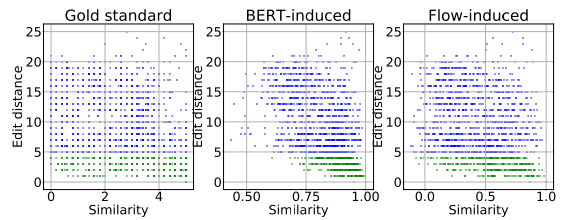
4. Lexical Similarity在不同模型中的规律实验

论文通过一组简单的对比实验，得出以下结论：

BERT-Induced Similarity的与Lexical Similarity存在着过度的相关性。

Flow-Induced Similarity 与Lexical Similarity的相关性较低。

方法是通过Similarity与Edit distance的对应关系，实验结果如图：

Confusion:

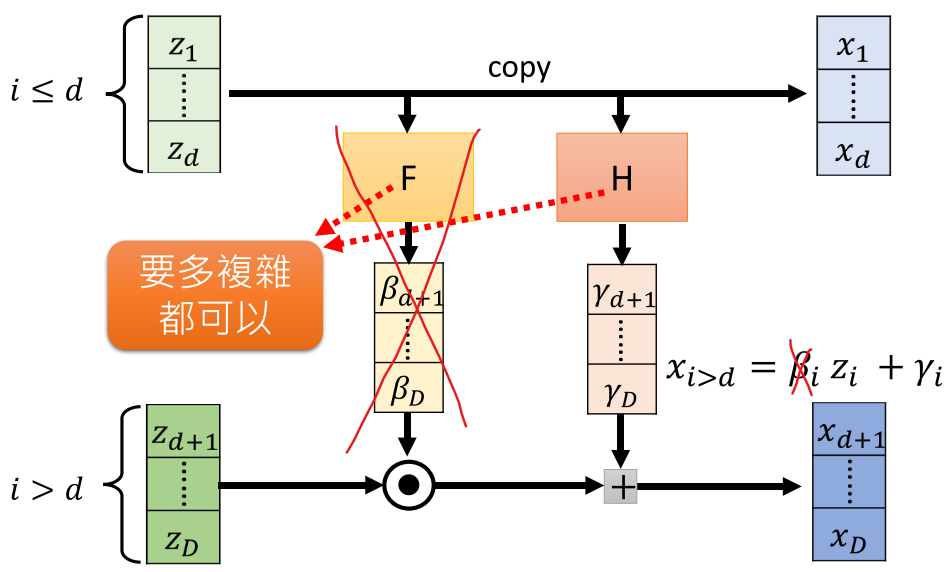
正交标准化？标准化协方差矩阵？

求一个线性变换\(W\)使得BERT输出的向量矩阵成一个标准化的矩阵。直接达到正交化的目的，是否也是可行？

首先求原始协方差矩阵： \[ \mu=\frac{1}{N}\sum_{k=1}^Nxi \] 那么 \[ \Sigma=\frac{1}{N}\sum_{k=1}^N(x_i-\mu)^T(x_i-\mu) \] 变换\(W\)满足： \[ W^T\Sigma W=I \] 其中\(\Sigma\)为一个正交对称矩阵。对其SVD，有如下关系： \[ \Sigma=U\Lambda U^T=(W^{-1})^TW^{-1} \] 得到变换\(W\)为： \[ W=U\sqrt{\Lambda^{-1}} \] 作者实验的结果显示，该方法简洁，且效果与flow模型相差无几。

作者称该方法为BERT-whitening。

核心代码：

1
2
3
4
5
6
7
def compute_w_bias(vecs, n_components):
    vecs = np.concatenate(vecs, axis=0)
    mu = vecs.mean(axis=0, keepdims=True)
    cov = np.cov(vecs.T)
    u, s, vh = np.linalg.svd(cov)
    W = np.np.dot(u, np.diag(1/np.sqrt(s)))
    return W[:, :n_components], -mu

标准化

1
2
3
4
def transform_and_normalize(vecs, kernel=None, bias=None):
    if not (kernel is None or bias is None):
        vecs = (vecs + bias).dot(kernel)
    return vecs / (vecs**2).sum(axis=1, keepdims=True)**0.5

实现细节

  1. 大语料计算内存问题？

句子向量均值递归计算 \[ \mu_{n+1}=\frac{n}{n+1}\mu_n+\frac{1}{n+1}x_{n+1} \] 协方差递归计算 \[ \Sigma_{n+1}=\frac{n}{n+1}\Sigma_n+\frac{1}{n+1}(x_{n+1}-\mu)^T(x_{n+1}-\mu) \]

  1. BERT模型在任务数据上，先微调

论文中先在任务数据上微调，比如先进行情感分类任务，再用来计算句子向量。

  1. flow做不到的简单的句子向量降维

SVD中直接取\(W\)前n个维度，即PCA，得到降维的结果。该结果将更具任务语境特征的维度提取出来。不仅提升了句子向量间相似度的速度，还可能提升预测的效果。

Notes NLP
sentence embedding BERT nlp

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！