数据结构整理-part1

导论

数据结构 是计算机存储、组织数据的方式，是指数据元素的集合以及数据元素之间存在的一种或者多种关系的集合

元素之间的关系包括数据的逻辑结构、数据的存储结构和数据的运算结构。

数据 是信息的载体，是可以被计算机识别存储并加工处理的描述客观事物的信息符号的总称。

数据元素 是数据的基本单位，在计算机程序中通常作为一个整体考虑。一个数据元素由若干个 数据项 组成。

数据项是数据结构中讨论的最小单位。有两类数据元素：如果数据元素不能再分，则称为 原子项 ；如果数据元素由若干个数据项组成，则称为 组合项 。

数据结构是一门研究非数值计算的学科，主要研究数据元素以及它们之间的关系和运算等，而且确保经过这些运算后所得到的新结构仍然是原来的结构类型。

数据结构有两个要素，一个是数据元素的集合，另一个是关系的集合。

  • 集合结构。数据元素属于同一个集合。
  • 线性结构。数据元素之间存在着一对一的关系。常见的有链表、队列、栈等。
  • 树形结构。数据元素之间存在着一对多的关系。常见的有二叉树、二叉查找树、平衡二叉查找树等。
  • 图形结构。数据元素之间存在着多对多的关系。

按照存储方式的不同，数据结构可以分为顺序存储结构和链式存储结构：

  • 顺序存储结构，表示数据元素在存储器中是连续存储的，可以用相对位置来表示数据元素之间的逻辑结构，如顺序表、队列、栈等。

  • 链式存储结构，每个数据元素里设置了一个指针用来指向另一个元素的存储地址，以此来表示数据元素之间的逻辑结构。

按照逻辑结构来分，数据结构可以分为线性结构和非线性结构

  • 如果数据元素之间存在一对一的关系，则称为线性结构
  • 否则称为非线性结构。集合结构、树形结构、图形结构都称为非线性结构。

算法（Algorithm）是对某一个或者某一类问题的解决方案的描述，根据问题的输入，在有限的计算时间里输出预期的结果。

算法有以下 5 个特征：

  • 有穷性。算法必须在执行有限个操作后终止。
  • 确切性。算法的每一个操作必须有明确的定义。
  • 输入项。算法有零个或多个输入，描述算法的初始状态。
  • 输出项。算法有一个或多个输出，没有输出的算法我们认为是没有意义的。
  • 可行性。算法的每个计算操作都可以在有限时间内完成。

数据结构描述了数据元素之间的逻辑关系，算法描述了数据元素的操作步骤，数据结构和算法组成了程序世界。数据结构和算法之间是不可分割的关系，数据结构是程序的基础，算法将数据互相联系起来，形成了一套能解决具体问题的方案。

在解决问题时，一般我们会优先确定数据结构，然后再来完善算法，有时也会反过来，根据算法来选择合适的数据结构。选择一个合适的数据结构，可以降低算法的复杂度，提高算法的效率。

复杂度分析

时间复杂度

时间频度是指算法中语句的执行次数，用 T(n) 来表示， n 为问题的规模。

时间频度的表达方法有点复杂，我们需要更直观的表达方法，于是引入了时间复杂度的概念。

函数 f(n)，在 n 趋向于无穷大时， T(n)/f(n) 的极限值为不等于 0 的常数，则我们近似的将 f(n) 替代 T(n)，记为 T(n)=O(f(n))，称为算法的渐进时间复杂度。

时间复杂度只关心算法中最耗时的部分

常见复杂度级别

空间复杂度

空间复杂度是指运行该算法所占用的存储空间大小，记为 S(n)

预估出算法运行所需的存储空间，包括指令空间、数据空间、动态申请的内存空间等。

1
2
3
4
5
int *a = new int[n];
int **b = new int*[n];
for (int i = 0; i < n; i++) {
    b[i] = new int[n];
}

S(n)=n+n^2，则空间复杂度为 O(n^2)。

内容

数据结构I 包含了一些基础的数据结构，一共分为三部分：

  • 线性结构，包括顺序表、链表、队列、栈等；
  • 树结构和图结构的入门，包括二叉树、图的存储方式等；
  • 查找排序算法，包括哈希表、顺序查找、折半查找、三分查找等查找算法，和插入排序、冒泡排序、归并排序、选择排序和快速排序等排序算法。

数据结构II 包含了一些进阶的数据结构，一共分为两部分：

  • 树结构，包括二叉查找树、平衡二叉查找树、堆与优先队列、森林与并查集等；
  • 图结构，包括图的遍历、图的连通性、最短路和最小生成树等算法。

线性表

线性表是由 相同数据类型 的 n 个数据元素组成的有限序列。

线性表按照存储结构，可以分为顺序表和链表两种类型。

顺序表

实现顺序表的构造、插入、扩容、查找、删除、遍历这 6 种基本操作，并在本章最后用顺序表这个数据结构求解一道题目

顺序表是线性表的一种顺序存储形式。换句话说，线性表是逻辑结构，表示元素之间一对一的相邻关系；而顺序表是存储结构，是指用一组地址连续的存储单元，依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。

顺序表在程序中通常用一维数组实现，一维数组可以是静态分配的，也可以是动态分配的。

在静态分配时，由于数组的大小和空间是固定的

在动态分配时，存储数组的空间在程序执行过程中会动态调整大小

  1. 支持随机访问
  2. 插入和删除操作需要移动大量的元素，从而保持逻辑上和物理上的连续性。

堆里数组，同时使用一段连续地址，储存相同类型的有限数据序列。

implement

实现一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct Vector {
    int size, length;
    int *data;
} Vector;

void init(Vector *vector, int size) {
    vector->size = size;
    vector->length = 0;
    vector->data = (int *)malloc(sizeof(int) * size);
}

// 请在下面实现扩容函数 expand
void expand(Vector *vector) {
    int *old_data = vector->data;
    vector->size = vector->size * 2;
    vector->data = (int *)malloc(sizeof(int) * vector->size);
    for (int i = 0; i < vector->length; ++i) {
        vector->data[i] = old_data[i];
    }
    free(old_data);
}

int insert(Vector *vector, int loc, int value) {
    if (loc < 0 || loc > vector->length) {
        return ERROR;
    }
    if (vector->length >= vector->size) {
        // return ERROR;
        expand(vector);
    }
    for (int i = vector->length; i > loc; --i) {
        vector->data[i] = vector->data[i - 1];
    }
    vector->data[loc] = value;
    vector->length++;
    return OK;
}

int search(Vector *vector, int value) {
    for (int i = 0; i < vector->length; ++i) {
        if (vector->data[i] == value) {
            return i;
        }
    }
    return -1;
}

int delete_node(Vector *vector, int index) {
    if (index < 0 || index >= vector->length) {
        return ERROR;   
    }
    for (int i = index + 1; i < vector->length; ++i) {
        vector->data[i - 1] = vector->data[i];
    }
    vector->length--;
    return OK;
}

void print(Vector *vector) {
    for (int i = 0; i < vector->length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", vector->data[i]);
    }
    printf("\n");
}

void clear(Vector *vector) {
    free(vector->data);
    free(vector);
}

int main() {
    Vector *a = (Vector *)malloc(sizeof(Vector));
    init(a, 100);
    printf("%d\n", insert(a, 1, 0));
    printf("%d\n", insert(a, 0, 1));
    printf("%d\n", insert(a, 2, 1));
    printf("%d\n", insert(a, 1, 2));
    printf("%d\n", insert(a, 0, 3));
    clear(a);
    return 0;
}
实现二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ERROR 0
#define OK 1

/*
错误处理还不严谨，使用mem操作，比上一个for循环高效
*/

typedef struct Vector {
    int s, l;
    int *d;
} Vector;

void init(Vector *v, int size) {
    if (!v) return;
    v->s = size;
    v->l = 0;
    v->d = (int *)malloc(size * sizeof(int));
}

int expand(Vector *v) {
    if (!v) return ERROR;
    int expandsize = v->s;
    int *tmp = NULL;
    while (expandsize) {
        // realloc, append v->d. If necessary, copy to a bigger memory block.
        tmp = (int *)realloc(v->d, sizeof(int) * (v->s + expandsize));
        if (tmp) break;
        expandsize >>= 2; 
    }
    if (!tmp) return ERROR;
    v->d = tmp;
    v->s += expandsize;
    // printf("Expand succeed");
    return OK;
}

int insert(Vector *v, int loc, int value) {
    if (!v) return ERROR;
    if (loc < 0 || loc > v->l) return ERROR;
    if (v->s <= v->l) {
        if (!expand(v)) return ERROR;
    }
    memcpy(v->d + loc + 1, v->d + loc, sizeof(int) * (v->l - loc));
    v->d[loc] = value;
    v->l++;
    return OK;
}

int search(Vector *v, int target) {
    if (!v) return ERROR;
    for (int i = 0; i < v->l; ++i) {
        if (*(v->d + i) == target)
            return i + 1; // return index begin from 1
    }
    return ERROR;
}

int delete_node(Vector *v, int loc) {
    if (!v) return ERROR;
    if (loc < 0 || loc >= v->l) return ERROR;
    memcpy(v->d + loc, v->d + loc + 1, sizeof(int) * (v->l - loc - 1));
    v->l--;
    return OK;
}

void print(Vector *v) {
    int *tmp = v->d;
    int i = 0;
    while (i < v->l) {
        (i > 0) && printf(" ");
        printf("%d", *tmp);
        ++i;
        ++tmp;
    }
    printf("\n");
}

void clear(Vector *v) {
    free(v->d);
    free(v);
}

int main() {
    Vector *v = (Vector *)malloc(sizeof(Vector));
    init(v, 20);
    
    // random test: use  #include <time.h>   srand(time(NULL));  op = rand() % 4; ...

    int n, op, loc, val;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &op);
        switch (op) {
            case 1:
                scanf("%d%d", &loc, &val);
                if (insert(v, loc, val))
                    printf("success\n");
                else
                    printf("failed\n");
                break;
            case 2:
                scanf("%d", &loc);
                if (delete_node(v, loc))
                    printf("success\n");
                else
                    printf("failed\n");
                break;
            case 3:
                scanf("%d", &val);
                if (search(v, val))
                    printf("success\n");
                else
                    printf("failed\n");
                break;
            case 4:
                print(v);
                break;
        }
    }

    clear(v);
    return 0;
}

链表

implement

注意没有单独定义 linked list 结构体，没有记录长度。

示例用代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <stdio.h>
#include <stdlib.h>

typedef struct Node{
    int data;
    struct Node *next;
}Node, *LinkedList;

LinkedList insert(LinkedList head, Node *node, int index) {
    if (head == NULL) {
        if (index != 0) {
            return head;
        }
        head = node;
        return head;
    }
    if (index == 0) {
        node->next = head;
        head = node;
        return head;
    }
    Node *current_node = head;
    int count = 0;
    while (current_node->next != NULL && count < index - 1) {
        current_node = current_node->next;
        count++;
    }
    if (count == index - 1) {
        node->next = current_node->next;
        current_node->next = node;
    }
    return head;
}

void output(LinkedList head) {
    if (head == NULL) {
        return;
    }
    Node *current_node = head;
    while (current_node != NULL) {
        printf("%d ", current_node->data);
        current_node = current_node->next;
    }
    printf("\n");
}

LinkedList delete_node(LinkedList head, int index) {
    if (head == NULL) {
        return head;
    }
    Node *current_node = head;
    int count = 0;
    if (index == 0) {
        head = head->next;
        free(current_node);
        return head;
    }
    // count < index - 1:  index 比 链表长度 大很多，count == index - 1 不会成立，这里就是要保证找到目标位置时，count == index - 1 成立
    while (current_node->next != NULL && count < index - 1) {
        current_node = current_node->next;
        count++;
    }
    // 停在要删除位置前一个，current_node->next != NULL 应该恒成立
    if (count == index - 1 && current_node->next != NULL) {
        Node *delete_node = current_node->next;
        current_node->next = delete_node->next;
        free(delete_node);
    }
    return head;
}

LinkedList reverse(LinkedList head) {
    if (head == NULL) {
        return head;
    }
    Node *next_node, *current_node;
    current_node = head->next;
    head->next = NULL;
    while (current_node != NULL) {
        next_node = current_node->next;
        current_node->next = head;
        head = current_node;
        current_node = next_node;
    }
    return head;
}

void clear(LinkedList head) {
    Node *current_node = head;
    while (current_node != NULL) {
        Node *delete_node = current_node;
        current_node = current_node->next;
        free(delete_node);
    }
}

int main() {
    LinkedList linkedlist = NULL;
    for (int i = 1; i <= 10; i++) {
        Node *node = (Node *)malloc(sizeof(Node));
        node->data = i;
        node->next = NULL;
        linkedlist = insert(linkedlist, node, i - 1);
    }
    output(linkedlist);
    linkedlist = delete_node(linkedlist, 9);
    output(linkedlist);
    
    linkedlist = reverse(linkedlist);
    output(linkedlist);
    
    clear(linkedlist);
    return 0;
}
循环链表约瑟夫环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <stdlib.h>

typedef struct Node{
    int data;
    struct Node *next;
}Node, *LinkedList;

LinkedList insert(LinkedList head, Node *node, int index) {
    if (head == NULL) {
        if (index != 0) {
            return head;
        }
        head = node;
        head->next = head;
        return head;
    }
    if (index == 0) {
        node->next = head->next;  // 循环
        head->next = node;
        return head;
    }
    Node *current_node = head->next;  // head为标记的尾节点
    int count = 0;
    while (current_node != head && count < index - 1) {
        current_node = current_node->next;
        count++;
    }
    if (count == index - 1) {
        node->next = current_node->next;
        current_node->next = node;
    }
    // 此时更新尾节点
    if (node == head->next) {
        head = node;
    }
    return head;
}

// 约瑟夫环
void output_josephus(LinkedList head, int m) {
    Node *current_node = head;
    head = NULL;
    while (current_node->next != current_node) {
        for (int i = 1; i < m; i++) {
            current_node = current_node->next;
        }
        printf("%d ", current_node->next->data);
        Node *delete_node = current_node->next;
        current_node->next = current_node->next->next;
        free(delete_node);
    }
    printf("%d\n", current_node->data);
    free(current_node);
}

int main() {
    LinkedList linkedlist = NULL;
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
        Node *node = (Node *)malloc(sizeof(Node));
        node->data = i;
        node->next = NULL;
        linkedlist = insert(linkedlist, node, i - 1);
    }
    output_josephus(linkedlist, m);
    return 0;
}

循环链表需要记录的是尾结点的位置。那么插入节点就不会循环一圈，才能找到尾结点。

增加 dummy node 的解法 单向
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct Node
{
    int val;
    struct Node *next;
} Node;

typedef struct List
{
    // Node *head; 改为 dummy node, 而不再是一个指针
    Node head;
    int len;
} List;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    return n;
}

void freeNode(Node *n) {
    if (n) free(n);
    return;
}

List *initList() {
    List *l = (List *)malloc(sizeof(List));
    l->head.next = NULL;
    l->len = 0;
    return l;
}

void freeList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *del_ = NULL;
    while (p) {
        del_ = p;
        p = p->next;
        free(del_);
    }
    free(l);
    return;
}

// 插入输入节点
int insertNode(List *l, int idx, Node *n) {
    if (!l) return 0;
    if (idx < 0 | idx > l->len) return 0;
    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    n->next = prev->next;
    prev->next = n;

    l->len++;
    return 1;
}

// 插入输入值
int insertValue(List *l, int idx, int val) {
    Node *n = initNode(val);
    if (!insertNode(l, idx, n)) {
        freeNode(n);
        return 0;
    }
    return 1;
}

// 删除
int erase(List *l, int idx) {
    if (!l) return 0;
    if (idx < 0 | idx >= l->len) return 0;

    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    Node *tmp = prev->next;
    prev->next = tmp->next;

    freeNode(tmp);
    l->len--;
    return 1;
}

int search(List *l, int idx) {
    if (!l) return -1;
    if (idx < 0 | idx >= l->len) return -1;

    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    return prev->next->val;
}

void showList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *tmp = &(l->head);

    printf("List+: [");
    while (p) {
        tmp = p;
        printf("%d->", p->val);
        p = p->next;
    }
    printf("NULL]\n");

    return;
}
增加 dummy node 的解法 双向
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct Node
{
    int val;
    struct Node *next;
    struct Node *prev;
} Node;

typedef struct List
{
    // Node *head; 改为 dummy node, 而不再是一个指针
    Node head;
    int len;
} List;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    n->prev = NULL;
    return n;
}

void freeNode(Node *n) {
    if (n) free(n);
    return;
}

List *initList() {
    List *l = (List *)malloc(sizeof(List));
    l->head.next = NULL;
    l->head.prev = NULL; // not necessarily
    l->len = 0;
    return l;
}

void freeList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *del_ = NULL;
    while (p) {
        del_ = p;
        p = p->next;
        free(del_);
    }
    free(l);
    return;
}

// 插入输入节点
int insertNode(List *l, int idx, Node *n) {
    if (!l) return 0;
    if (idx < 0 | idx > l->len) return 0;
    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    n->next = prev->next;
    prev->next = n;

    n->prev = prev;
    if (n->next)
        n->next->prev = n;

    l->len++;
    return 1;
}

// 插入输入值
int insertValue(List *l, int idx, int val) {
    Node *n = initNode(val);
    if (!insertNode(l, idx, n)) {
        freeNode(n);
        return 0;
    }
    return 1;
}

// 删除
int erase(List *l, int idx) {
    if (!l) return 0;
    if (idx < 0 | idx >= l->len) return 0;

    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    Node *tmp = prev->next;
    prev->next = tmp->next;

    if (tmp->next)
        tmp->next->prev = prev;

    freeNode(tmp);
    l->len--;
    return 1;
}

int reverse(List *l) {
    if (!l || l->len == 0) return 0;

    Node *p = l->head.next;
    Node *cur = NULL;

    l->head.next = NULL;
    l->len = 0;
    while (p) {
        cur = p;
        p = p->next;
        insertNode(l, 0, cur);
    }

    return 1;
}

void showList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *tmp = &(l->head);
    int len = l->len;

    // printf("List+: [");
    // while (len--) {
    //     tmp = p;
    //     printf("%d->", p->val);
    //     p = p->next;
    // }
    // printf("NULL]\n");

    // printf("List-: [");
    // len = l->len;
    // while (len--) {
    //     printf("%d->", tmp->val);
    //     tmp = tmp->prev;
    // }
    // printf("HEAD]\n");

    printf("List+: [");
    while (p) {
        tmp = p;
        printf("%d->", p->val);
        p = p->next;
    }
    printf("NULL]\n");

    printf("List-: [");
    while (tmp != &(l->head)) {
        printf("%d->", tmp->val);
        tmp = tmp->prev;
    }
    printf("HEAD]\n");

    return;
}

int main(int argc, char **argv) {
    srand(time(NULL));
    int cnt = 20;
    List *l = initList();
    while (cnt--) {
        int val = rand() % 100;
        int opt = rand() % 5;
        int idx = rand() % (l->len + 3) - 1;

        switch (opt) {
            case 0:
            case 1:
            case 2:
                printf("insert %d at %d, res = %s\n", val, idx,
                        insertValue(l, idx, val) ? "SUCCESS" : "FAILED");
                break;
            case 3:
                printf("erease at %d, res = %s\n", idx,
                        erase(l, idx) ? "SUCCESS" : "FAILED");
                break;
            case 4:
                printf("reverse, res = %s\n",
                        reverse(l) ? "SUCCESS" : "FAILED");
                break;
        }
        showList(l);
        printf("\n");
    }

    return 0;
}

练习

LeetCode 剑指offer： 24 35 18 06 25 22 36 52

顺序表循环左移

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ERROR 0
#define OK 1

typedef struct Vector {
    int size, len;
    int *data;
} Vec;

void initVec(Vec *v, int size) {
    if (!v) return;
    v->size = size;
    v->len = 0;
    v->data = (int *)malloc(sizeof(int) * size);
    return;
}

int expand(Vec *v) {
    int asize = v->size;
    int *tmp = NULL;
    while (asize) {
        tmp = (int *)realloc(v->data, sizeof(int) * (asize + v->size));
        if (tmp) break;
        asize >>= 2;
    }
    if (tmp == NULL) return ERROR;
    v->data = tmp;
    v->size += asize;
    return OK;
}

int insert(Vec *v, int idx, int val) {
    if (!v) return ERROR;
    if (idx < 0 | idx > v->len) return ERROR;
    if (v->size == v->len) 
        if (!expand(v)) return ERROR;
    memcpy(v->data + idx + 1, v->data + idx, sizeof(int) * (v->len - idx));
    v->data[idx] = val;
    v->len++;
    return OK;
}

void freeVec(Vec *v) {
    if (!v) return;
    free(v->data);
    free(v);
}

// move
int moveBlock(Vec *v, int num) {
    if (!v) return ERROR;
    if (num < 0 | num > v->len) return ERROR;
    int *tmp = (int *)malloc(num * sizeof(int));
    memcpy(tmp, v->data, sizeof(int) * num);
    memcpy(v->data, v->data + num, sizeof(int) * (v->len - num));
    memcpy(v->data + (v->len - num), tmp, sizeof(int) * num);
    return OK;
}

void printVec(Vec *v) {
    if (!v) return;
    for (int i = 0; i < v->len; i++) {
        (i > 0) && printf(" ");
        printf("%d", *(v->data + i));
    }
    return;
}

int main() {
    Vec *v = (Vec *)malloc(sizeof(Vec));
    (void)initVec(v, 10);
    int n, k, val;
    scanf("%d%d", &n, &k);
    for (int i=0; i<n; i++) {
        scanf("%d", &val);
        if (!insert(v, i, val)) return 3;
    }
    if (!moveBlock(v, k)) return 4;
    (void)printVec(v);
    (void)freeVec(v);
    return 0;
}

reverse chars

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct Node
{
    int val;
    struct Node *next;
} Node;

typedef struct List
{
    // Node *head; 改为 dummy node, 而不再是一个指针
    Node head;
    int len;
} List;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    return n;
}

void freeNode(Node *n) {
    if (n) free(n);
    return;
}

List *initList() {
    List *l = (List *)malloc(sizeof(List));
    l->head.next = NULL;
    l->len = 0;
    return l;
}

void freeList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *del_ = NULL;
    while (p) {
        del_ = p;
        p = p->next;
        free(del_);
    }
    free(l);
    return;
}

// 插入输入节点
int insertNode(List *l, int idx, Node *n) {
    if (!l) return 0;
    if (idx < 0 | idx > l->len) return 0;
    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    n->next = prev->next;
    prev->next = n;

    l->len++;
    return 1;
}

// 插入输入值
int insertValue(List *l, int idx, int val) {
    Node *n = initNode(val);
    if (!insertNode(l, idx, n)) {
        freeNode(n);
        return 0;
    }
    return 1;
}

// 实现reverse
int reverse(List *l) {
    if (!l) return 0;
    Node *cur = l->head.next;
    Node *tmp = NULL;
    l->head.next = NULL;
    l->len = 0;
    while (cur) {
        tmp = cur;
        cur = cur->next;
        tmp->next = l->head.next;
        l->head.next = tmp;
        l->len++;
    }
    return 1;
}

int search(List *l, int idx) {
    if (!l) return -1;
    if (idx < 0 | idx >= l->len) return -1;

    Node *prev = &(l->head);
    while (idx--)
        prev = prev->next;

    return prev->next->val;
}

void showList(List *l) {
    if (!l) return;
    Node *p = l->head.next;

    while (p) {
        printf("%c", p->val);
        p = p->next;
        (p != NULL) && printf(" ");
    }

    return;
}

int main() {
    int n;
    char c;
    scanf("%d", &n);
    List *l = initList();

    getchar();
    for (int i=0; i<n * 2 - 1; i++) {
        scanf("%c", &c);
        if (c > 40) {
            if (!insertValue(l, i / 2, c)) return 1;
        }
    }

    if (!reverse(l)) return 2;
    (void)showList(l);

    freeList(l);

    return 0;
}

双向循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct Node
{
    int val;
    struct Node *next;
    struct Node *prev;
} Node;

typedef struct List
{
    // Node *head; 改为 dummy node, 而不再是一个指针
    Node head;
    int len;
} List;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    n->prev = NULL;
    return n;
}

void freeNode(Node *n) {
    if (n) free(n);
    return;
}

List *initList() {
    List *l = (List *)malloc(sizeof(List));
    l->head.next = NULL;
    l->head.prev = NULL; // not necessarily
    l->len = 0;
    return l;
}

void freeList(List *l) {
    if (!l) return;
    Node *p = l->head.next;
    Node *del_ = NULL;
    int len = l->len;
    while (len) { // 更改为按长度free
        del_ = p;
        p = p->next;
        free(del_);
        len--;
    }
    free(l);
    return;
}

// 插入输入节点: 更改为循环链表
int insertNode(List *l, int idx, Node *n) {
    if (!l) return 0;
    if (idx < 0 | idx > l->len) return 0;

    if (l->len == 0) {
        l->head.next = n;
        n->prev = n;
        n->next = n;
        l->len++;
        return 1;
    }

    Node *prev = l->head.next;
    while (idx--)
        prev = prev->next;

    n->next = prev->next;
    prev->next = n;

    n->prev = prev;
    if (n->next)
        n->next->prev = n;

    if (n == l->head.next->next) {
        l->head.next = n;
    }

    l->len++;
    return 1;
}

// 插入输入值
int insertValue(List *l, int idx, int val) {
    Node *n = initNode(val);
    if (!insertNode(l, idx, n)) {
        freeNode(n);
        return 0;
    }
    return 1;
}

// 更改为循环链表 从 k 位置反向输出
void showList(List *l, int k) {
    if (!l) return;
    Node *p = l->head.next;
    int c = l->len;
    while (p->val != k && c) {
        p = p->next;
        c--;
    }
    if (c == 0 && p->val != k) return;

    Node *tmp = p;
    int len = l->len;

    while (tmp != p->next) {
        printf("%d ", tmp->val);
        tmp = tmp->prev;
    }
    printf("%d", p->next->val);
    return;
}

int main(int argc, char **argv) {
    int n, val;
    scanf("%d", &n);

    List *l = initList();
    for (int i = 0; i < n; i++) {
        scanf("%d", &val);
        insertValue(l, i, val);
    }

    int k;
    scanf("%d", &k);
    showList(l, k);

    freeList(l);
    return 0;
}

队列

队列有一个很重要的性质，就是 先进先出 ，First In First Out(FIFO)。

利用两个变量head和tail维护队列的进出。

简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct Queue{
    int *data;
    int head, tail, length;
}Queue;

void init(Queue *q, int length) {
    q->data = (int *)malloc(sizeof(int) * length);
    q->head = 0;
    q->tail = -1;
    q->length = length;
}

int push(Queue *q, int element) {
    if (q->tail + 1 >= q->length) return 0;
    q->data[++q->tail] = element;
    return 1;    
}
void output(Queue *q) {
    for (int i = q->head; i <= q->tail; ++i) {
        (i != q->head) && printf(" ");
        printf("%d", q->data[i]);
    }
}
int front(Queue *q) {
    return q->data[q->head];
}
void pop(Queue *q) {
    q->head++;
}

int empty(Queue *q) {
    return q->head > q->tail;
}

void clear(Queue *q) {
    free(q->data);
    free(q);
}

int main() {
    Queue *queue = (Queue *)malloc(sizeof(Queue));
    init(queue, 100);
    int n, val;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &val);
        if (!push(queue, val)) return 1;
    }

    if (!empty(queue)) {
        int k;
        scanf("%d", &k);
        while (k--) {
            pop(queue);
        }
    }
    
    if (!empty(queue)) {
        printf("%d\n", front(queue));
        output(queue);
    } else {
        printf("0");
    }
    
    clear(queue);
    return 0;
}

循环队列

在循环队列里，不能单纯通过比较 tail 和 head 标记来判断循环队列是否已满，否则在初始化状态就会被认为循环队列已满。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct Queue {
    int *data;
    int head, tail, length, count;
}Queue;

void init(Queue *q, int length) {
    q->data = (int *)malloc(sizeof(int) * length);
    q->length = length;
    q->head = 0;
    q->tail = -1;
    q->count = 0;
}

// 扩容需要考虑循环结构
int expand(Queue *q) {
    if (!q) return ERROR;
    int expsize = q->length;
    int *tmp = NULL;
    while (expsize > 0) {
        // 因为要重新组织数据，所以不用realloc了
        tmp = (int *)malloc(sizeof(int) * (q->length + expsize));
        if (tmp) break;
        expsize >>= 1;
    }
    if (!tmp) return ERROR;

    // 复制到新空间中
    int i, j;
    int end = (q->tail + 1) % q->length;
    for (i = q->head, j = 0; i != end; i = (i + 1) % q->length, j++) {
        tmp[j] = q->data[i];
    }
    free(q->data);
    q->data = tmp;
    q->length += expsize;
    q->head = 0;
    q->tail = j - 1;
    return OK;
}

int push(Queue *q, int element) {
    if (q->count >= q->length) {
        if (!expand(q))
            return ERROR;
    }
    q->tail = (q->tail + 1) % q->length; // 环 取余
    q->data[q->tail] = element;
    q->count++;
    return OK;
}

void output(Queue *q) {
    int i = q->head; // 从 head 到 tail
    do {
        printf("%d ", q->data[i]);
        i = (i + 1) % q->length;
    } while(i != (q->tail + 1) % q->length);
    printf("\n");
}

int front(Queue *q) {
    return q->data[q->head];
}

void pop(Queue *q) {
    q->head = (q->head + 1) % q->length; // 环 取余
    q->count--;
}

int empty(Queue *q) {
    return q->count == 0;
}

void clear(Queue *q) {
    free(q->data);
    free(q);
}

int main() {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    init(q, 100);
    for (int i = 1; i <= 10; i++) {
        push(q, i);
    }
    output(q);
    if (!empty(q)) {
        printf("%d\n", front(q));
        pop(q);        
    }
    output(q);
    clear(q);
    return 0;
}

链表实现队列

链表使用了一个dummy node.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>


#define ERROR 0;
#define OK 1;


typedef struct Node {
    int val;
    struct Node *next;
} Node, *Node_p;

// 设计为带有dummy head的链表
typedef struct Queue {
    Node *head;
    Node *tail;
    int len;
} Queue, *Queue_p;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    return n;
}

Queue *initStack() {
    Queue_p q = (Queue_p)malloc(sizeof(Queue));
    q->head = initNode(-1);
    q->tail = NULL;
    q->len = 0;
    return q;
}

int push(Queue_p q, int val) {
    if (!q) return ERROR;
    Node_p node = initNode(val);

    // 有tail就在tail之后增加
    if (q->tail) {
        q->tail->next = node;
        q->tail = node;
    } else {
        node->next = q->head->next;
        q->head->next = node;
        q->tail = node;
    }
    q->len++;

    return OK;
}

void freeNode(Node_p n) {
    if (n) free(n);
}

int pop(Queue_p q) {
    if (!q || !q->head || !q->head->next) return ERROR;
    Node_p tmp = q->head->next;
    q->head->next = q->head->next->next;
    freeNode(tmp);

    // 最后一个节点被弹出
    if (q->head->next == NULL)
        q->tail = NULL;

    q->len--;
    return OK;
}

int top(Queue_p q) {
    if (!q || !q->head || !q->head->next) return ERROR;
    return q->head->next->val;
}

int empty(Queue_p q) {
    return (!q || !q->head || !q->head->next);
}

void freeStack(Queue_p q) {
    if (!q || !q->head) return;
    Node *p = q->head, *tmp;
    while (p) {
        tmp = p;
        p = p->next;
        freeNode(tmp);
    }
    free(q);
}

void showStack(Queue_p q) {
    if (!q || !q->head) return;
    Node_p p = q->head->next;
    while (p) {
        (p != q->head->next) && printf(" ");
        printf("%d", p->val);
        p = p->next;
    }
    printf("\n");
}

int main() {
    srand(time(NULL));
    Queue_p q = initStack();
    int cnt = 20;
    while (cnt--) {
        int val = rand() % 100;
        int opt = rand() % 4;
        switch (opt) {
            case 0:
            case 1:
            case 2:
                printf("push %d, %s\n", val, push(q, val) ? "SUC": "ERROR");
                showStack(q);
                break;
            case 3:
                empty(q) ? printf("Nothing to pop.\n") : printf("Pop.\n");
                pop(q);
                showStack(q);
                break;
        }
    }
    printf("\nFinal: \n");
    showStack(q);
    return 0;
}

栈

栈有一个重要的性质，就是 先进后出 ，First In Last Out(FILO)。例如，浏览器页面的多次跳转和多次返会功能，就是栈的应用。

利用一个变量维护栈顶位置。

栈，通过实现一个表达式解析问题，进行实现。

用栈实现表达式求值的算法流程如下：

  1. 使用两个栈分别存储数值和运算符。
  2. 读取表达式字符，数值存入数值栈，运算符和栈顶运算符比较优先级。
  3. 通过运算符优先级不同选择将它压入栈或取出数值栈中两个元素进行计算，计算结果入栈。
  4. 返回步骤 2，直至表达式全部读完。
  5. 弹出一个运算符和两个数值进行运算，计算结果存储数值栈。
  6. 当运算符栈不为空时，返回步骤 5，否则数值栈中剩余的最后一个元素就是表达式求值结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>

#define ERROR 0
#define OK 1

typedef struct Stack {
    int *elements;
    int max_size, top_index;
} Stack;

void init(Stack *s, int length) {
    s->elements = (int *)malloc(sizeof(int) * length);
    s->max_size = length;
    s->top_index = -1;
}

int expand(Stack *s) {
    if (!s) return ERROR;
    int expsize = s->max_size;
    int *tmp;
    while (expsize > 0) {
        tmp = (int *)realloc(s->elements, sizeof(int) * (s->max_size + expsize));
        if (tmp) break;
        expsize >>= 1;
    }
    if (!tmp) return ERROR;

    s->elements = tmp;
    s->max_size += expsize;

    return OK;
}

int push(Stack *s, int element) {
    if (s->top_index >= s->max_size - 1) {
        if (!expand(s))
            return ERROR;
    }
    s->top_index++;
    s->elements[s->top_index] = element;
    return OK;
}

int pop(Stack *s) {
    if (s->top_index < 0) {
        return ERROR;
    }
    s->top_index--;
    return OK;
}

int top(Stack *s) {
    return s->elements[s->top_index];
}

int empty(Stack *s) {
    if (s->top_index < 0) {
        return 1;
    } else {
        return 0;
    }
}

// 优先级判断
int precede(char a, char b) {
    if ((a == '*'||a=='/') && (b == '+'||b == '-')) {
        return 1;
    } else {
        return 0;
    }
}

// 计算 a theta b
int operate(char theta, int a, int b) {
    if (theta == '+') {
        return a + b;
    } else if (theta == '*'){
        return a * b;
    } else if (theta == '-'){
        return a - b;
    } else if (theta == '/'){
        return a / b;
    }
}

// 计算表达式
void calc(Stack *numbers, Stack *operators) {
    int a = top(numbers);
    pop(numbers);
    int b = top(numbers);
    pop(numbers);
    push(numbers, operate(top(operators), b, a));
    pop(operators);
}

void clear(Stack *s) {
    free(s->elements);
    free(s);
}

int main() {
    int n;
    scanf("%d", &n);
    Stack *numbers = (Stack *)malloc(sizeof(Stack));
    init(numbers, n);
    Stack *operators = (Stack *)malloc(sizeof(Stack));
    init(operators, n);
    
    char *buffer = (char *)malloc(sizeof(char) * (n + 1));
    scanf("%s", buffer);
    
    int i = 0;
    while (i < n) {
        if (isdigit(buffer[i])) {
            push(numbers, buffer[i] - '0');
            i++;
        } else {
            if (empty(operators) || precede(buffer[i], top(operators))) {
                push(operators, buffer[i]);
                i++;
            } else {
                calc(numbers, operators);
            }
        }
    }
    while (!empty(operators)) {
        calc(numbers, operators);
    }
    printf("%d\n", top(numbers));
    clear(numbers);
    clear(operators);
    free(buffer);
    return 0;
}

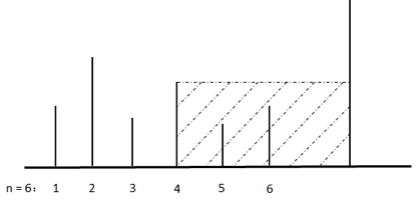
单调栈

地上从左到右竖立着 n 块木板，从 1 到 n 依次编号，如下图所示。我们知道每块木板的高度，在第 n 块木板右侧竖立着一块高度无限大的木板，现对每块木板依次做如下的操作：对于第 i 块木板，我们从其右侧开始倒水，直到水的高度等于第 i 块木板的高度，倒入的水会淹没 \(a_i\) 块木板（如果木板左右两侧水的高度大于等于木板高度即视为木板被淹没）。求 n 次操作后，所有 \(a_i\) 的和是多少。

如图所示，在第 4 块木板右侧倒水，可以淹没第 5 块和第 6 块一共 2 块木板，\(a_4\) = 2。

例图

建立一个从栈顶到栈底递增的单调栈。假设木板p是栈顶元素，木板q是当前待入栈元素。

将q push 到栈的过程中，如果栈顶元素p出栈则表明我们已经找到了木板p右侧第一块比它高的木板q。

然后只需要记录q与p之间的木板数，求和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct Node {
    int id, height;
} Node;

typedef struct Stack {
    Node *elements;
    int max_size, top_index;
} Stack;

void init(Stack *s, int length) {
    s->elements = (Node *)malloc(sizeof(Node) * length);
    s->max_size = length;
    s->top_index = -1;
}

int push(Stack *s, Node element) {
    if (s->top_index >= s->max_size - 1) {
        return ERROR;
    }
    s->top_index++;
    s->elements[s->top_index] = element;
    return OK;
}

int pop(Stack *s) {
    if (s->top_index < 0) {
        return ERROR;
    }
    s->top_index--;
    return OK;
}

Node top(Stack *s) {
    return s->elements[s->top_index];
}

int empty(Stack *s) {
    if (s->top_index < 0) {
        return 1;
    } else {
        return 0;
    }
}

void clear(Stack *s) {
    free(s->elements);
    free(s);
}

int main() {
    int n, ans = 0;
    scanf("%d", &n);
    Stack *stack = (Stack *)malloc(sizeof(Stack));
    init(stack, n);
    Node temp;
    
    for (int i = 1; i <= n; i++) {
        scanf("%d", &temp.height);
        temp.id = i;
        while (!empty(stack) && top(stack).height <= temp.height) {
            ans = ans + i - top(stack).id - 1;
            pop(stack);
        }
        push(stack, temp);
    }
    while (!empty(stack)) {
        ans = ans + n + 1 - top(stack).id - 1;
        pop(stack);
    }
    printf("%d\n", ans);
    clear(stack);
    return 0;
}

链表实现栈

使用一个带有dummy node的链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <time.h>


#define ERROR 0;
#define OK 1;


typedef struct Node {
    int val;
    struct Node *next;
} Node, *Node_p;

// 设计为带有dummy head的链表
typedef struct Stack {
    Node *head;
    int len;
} Stack, *Stack_p;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->next = NULL;
    return n;
}

Stack *initStack() {
    Stack_p s = (Stack_p)malloc(sizeof(Stack));
    s->head = initNode(-1);
    s->len = 0;
    return s;
}

int push(Stack_p s, int val) {
    if (!s) return ERROR;
    Node_p node = initNode(val);
    node->next = s->head->next;
    s->head->next = node;
    s->len++;
    return OK;
}

void freeNode(Node_p n) {
    if (n) free(n);
}

int pop(Stack_p s) {
    if (!s || !s->head || !s->head->next) return ERROR;
    Node_p tmp = s->head->next;
    s->head->next = s->head->next->next;
    freeNode(tmp);
    s->len--;
    return OK;
}

int top(Stack_p s) {
    if (!s || !s->head || !s->head->next) return ERROR;
    return s->head->next->val;
}

int empty(Stack_p s) {
    return (!s || !s->head || !s->head->next);
}

void freeStack(Stack_p s) {
    if (!s || !s->head) return;
    Node *p = s->head, *tmp;
    while (p) {
        tmp = p;
        p = p->next;
        freeNode(tmp);
    }
    free(s);
}

void showStack(Stack_p s) {
    if (!s || !s->head) return;
    Node_p p = s->head->next;
    while (p) {
        (p != s->head->next) && printf(" ");
        printf("%d", p->val);
        p = p->next;
    }
    printf("\n");
}

int main() {
    srand(time(NULL));
    Stack_p s = initStack();
    int cnt = 20;
    while (cnt--) {
        int val = rand() % 100;
        int opt = rand() % 4;
        switch (opt) {
            case 0:
            case 1:
            case 2:
                printf("push %d, %s\n", val, push(s, val) ? "SUC": "ERROR");
                showStack(s);
                break;
            case 3:
                empty(s) ? printf("Nothing to pop.\n") : printf("Pop.\n");
                pop(s);
                showStack(s);
                break;
        }
    }
    printf("\nFinal: \n");
    showStack(s);
    return 0;
}

树

定义

基本概念

分支度：节点拥有的子节点个数。

阶层：从根节点层往下，阶层从 1 往下依次增加。

高度（深度）：树的最大阶层值。⾼度和深度是相反的， ⾼度是从下往上数， 深度是从上往 下。 因此根节点的深度和叶⼦节点的⾼度是 1。

祖先：某节点到根节点的路径上所有节点都是该节点祖先。

树林：多个数的集合。

歪斜树：所有节点只有左孩子，左歪斜树。右歪斜树同理。

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。 也就是说，如果一个二叉树的层数为 k，且结点总数是\(2^k -1\) ，则它就是满二叉树。

完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

性质

  1. 二叉树第 i 层对多 \(2^{i-1}\) 个节点。
  2. 层数为 k 的满二叉树节点数为 \(2^k -1\)。
  3. 二叉树中，终端节点个数，等于度数为 2 的节点个数 + 1。

遍历

先序遍历时，遍历的顺序是从根结点开始，先访问当前结点，如果左子树不为空则继续访问左子树，之后若右子树不为空再访问右子树。在左右子树中依然按照这样的顺序进行遍历。

中序遍历的顺序是从当前结点的左子树开始遍历，再访问当前结点，最后访问右子树。

后序遍历先访问当前结点的左子树，再访问右子树，最后访问当前结点。

简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node *lchild, *rchild;
} Node;

typedef struct Tree {
    int len;
    Node *root;
} Tree;

Node* init(int data) {
    Node *node =(Node *)malloc(sizeof(Node));
    node->data = data;
    node->lchild = NULL;
    node->rchild = NULL;
    return node;
}

// 保持二叉搜索树结构，插入值
Node *insert(Node *root, int val) {
    if (!root) {
        Node *n =  init(val);
        return n;
    }

    if (root->data < val) {
        root->rchild = insert(root->rchild, val);
    } else {
        root->lchild = insert(root->lchild, val);
    }

    return root;
}

// 保持二叉搜索树结构，插入值. 不返回指针，直接在原地址中操作。
void insert_no_return(Node **raddr, int val) {
    if (!(*raddr)) {
        *raddr =  init(val);
        return;
    }

    if ((*raddr)->data < val) {
        (*raddr)->rchild = insert(&((*raddr)->rchild), val);
    } else {
        (*raddr)->lchild = insert(&((*raddr)->lchild), val);
    }

    return;
}

void insert_tree(Tree *t, int val) {
    if (!t) return;
    t->root = insert(t->root, val);
    t->len++;
}

Node* build_demo() {
    Node *node = init(1);
    node->lchild = init(2);
    node->rchild = init(3);
    node->lchild->lchild = init(4);
    node->lchild->rchild = init(5);
    node->rchild->rchild = init(6);
    return node;
}

void preorder(Node *node) {
    printf("%d ", node->data);
    if (node->lchild != NULL) {
        preorder(node->lchild);
    }
    if (node->rchild != NULL) {
        preorder(node->rchild);
    }
}

void inorder(Node *node) {
    if (node->lchild != NULL) {
        inorder(node->lchild);
    }
    printf("%d ", node->data);
    if (node->rchild != NULL) {
        inorder(node->rchild);
    }
}

void postorder(Node *node) {
    if (node->lchild != NULL) {
        postorder(node->lchild);
    }
    if (node->rchild != NULL) {
        postorder(node->rchild);
    }
    printf("%d ", node->data);
}


void clear(Node *node) {
    if (node->lchild != NULL) {
        clear(node->lchild);
    }
    if (node->rchild != NULL) {
        clear(node->rchild);
    }
    free(node);
}

void clear_tree(Tree *t) {
    if (t->root)
        clear(t->root);
    free(t);
    return;
}

已知先序和中序求后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct Node {
    int data;
    struct Node *lchild, *rchild;
} Node;

Node* init(int data) {
    Node *node =(Node *)malloc(sizeof(Node));
    node->data = data;
    node->lchild = NULL;
    node->rchild = NULL;
    return node;
}

void postorder(Node *node) {
    if (node->lchild != NULL) {
        postorder(node->lchild);
    }
    if (node->rchild != NULL) {
        postorder(node->rchild);
    }
    printf("%d ", node->data);
}

// 根据先序和中序建立二叉树的函数 build
Node *build(char pre_str[], char in_str[], int len) {
    Node *p = init(pre_str[0] - '0');
    int pos = strchr(in_str, pre_str[0]) - in_str;
    if (pos > 0) {
        p->lchild = build(pre_str + 1, in_str, pos);
    }
    if (len - pos - 1 > 0) {
        p->rchild = build(pre_str + pos + 1, in_str + pos + 1, len - pos - 1);
    }
    return p;
}


void clear(Node *node) {
    if (node->lchild != NULL) {
        clear(node->lchild);
    }
    if (node->rchild != NULL) {
        clear(node->rchild);
    }
    free(node);
}

int main() {
    char pre_str[] = "136945827";
    char in_str[] = "963548127";
    
    Node *root = build(pre_str, in_str, strlen(pre_str));
    postorder(root);
    printf("\n");
    
    clear(root);
    return 0;
}

Huffman编码

1952 年由 David A. Huffman 提出的一种无损数据压缩的编码算法。

哈夫曼编码先统计出每种字母在字符串里出现的频率，根据频率建立一棵路径带权的二叉树，也就是哈夫曼树。

树上每个结点存储字母出现的频率，根结点到结点的路径即是字母的编码，频率高的字母使用较短的编码，频率低的字母使用较长的编码，这样使得编码后的字符串占用空间最小。

实现方法

首先统计每个字母在字符串里出现的频率，把每个字母看成一个结点，结点的权值即是字母出现的频率。

把每个结点看成一棵只有根结点的二叉树，一开始把所有二叉树（结点）都放在一个集合里，接下来开始如下编码：

步骤一：从集合里取出两个根结点权值最小的树a和b，构造出一棵新的二叉树c，二叉树c的根结点的权值为a和b的根结点权值和，二叉树c的左右子树分别是a和b。（合并）

步骤二：将二叉树a和b从集合里删除，把二叉树c加入集合里。（更新候选）

重复以上两个步骤，直到集合里只剩下一棵二叉树，最后剩下的就是哈夫曼树了。

规定每个有孩子的结点，到左孩子的路径为 0，到右孩子的路径为 1。每个字母的编码就是根结点到字母对应结点的路径。

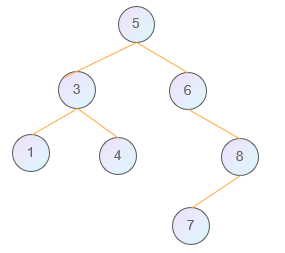
广义表

示例：

示例

广义表为：(5 ( 3 ( 1, 4 ), 6 (, 8 ( 7, ) ) ) )

实现根据广义表输入，构建树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
...
// 上接树的实现    

#include <string.h>
// 栈处理广义表
typedef struct Stack {
    Node **elements;
    int max_size, top_index;
} Stack;

Stack *init_stack(int length) {
    Stack *s = (Stack *)malloc(sizeof(Stack));
    s->elements = (Node **)malloc(sizeof(Node *) * length);
    s->max_size = length;
    s->top_index = -1;
    return s;
}

void freeStack(Stack *s) {
    if (!s) return;
    free(s->elements);
    free(s);
}

int push(Stack *s, Node *n) {
    if (!s) return 0;
    if (s->top_index == s->max_size - 1) return 0;
    s->elements[++s->top_index] = n;
    return 1;
}

int is_empty(Stack *s) {
    return !(s && s->top_index != -1);
}

Node *pop(Stack *s) {
    return s->elements[s->top_index--];
}

Node *build_tree(char *str) {
    Stack *s = init_stack(100);
    Node *root, *n;
    int flag = 0;

    while(str[0]) {
        switch (str[0]) {
            case '(':
                push(s, n);
                flag = 0;
                break;
            case ',':
                flag = 1;
                break;
            case ')':
                root = pop(s);
                break;
            default:
                if (str[0] < '0' || str[0] > '9') break;

                int num = 0;
                while (str[0] >= '0' && str[0] <= '9') {
                    num = num * 10 + (str[0] - '0');
                }
                str--;
                n = init(num);

                if (!is_empty(s))
                    flag ? (s->elements[s->top_index]->rchild = n) : \
                           (s->elements[s->top_index]->lchild = n);
        }
        ++str;
    }

    freeStack(s);
    return root;
}

线索二叉树

利用叶子节点的空指针，建立所需要的前驱后继结构。比如下面实现中序遍历的前驱后继。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// ltag 和 rtag 表示节点的左右孩子是普通孩子节点还是前驱后继节点。
// 前驱后继节点，将叶子节点的空指针孩子指向中序遍历的前驱后继节点。
enum {
    CHILD = 0,
    THREAD = 1
};

typedef struct Node {
    int val;
    struct Node *lchild;
    struct Node *rchild;
    int rtag, ltag;
} Node;

Node *initNode(int val) {
    Node *n = (Node *)malloc(sizeof(Node));
    n->val = val;
    n->lchild = NULL;
    n->rchild = NULL;
    n->ltag = CHILD;
    n->rtag = CHILD;
    return n;
}

void freeNode(Node *n) {
    if (!n) return;
    free(n);
    return;
}

Node *insert(Node *root, int val) {
    if (!root) return initNode(val);
    if (val > root->val)
        root->rchild = insert(root->rchild, val);
    else
        root->lchild = insert(root->lchild, val);
    return root;
}

void freeTree(Node *root) {
    if (!root) return;
    if (root->rtag == CHILD)
        freeTree(root->rchild);
    if (root->ltag == CHILD)
        freeTree(root->lchild);
    freeNode(root);
    return;
}

void inorder(Node *root) {
    if (!root) return;
    if (root->ltag == CHILD)
        inorder(root->lchild);
    if (root->rtag == CHILD)
        printf("%d ", root->val);
    inorder(root->rchild);
    return;
}


// 线索二叉树
Node *pre = NULL;

// 类似inordoer的遍历方法，同时更新叶子节点的前驱和后继
void build_thread_tree(Node *root) {
    if (!root) return;

    build_thread_tree(root->lchild);

    // 更新当前节点（叶子节点）的前驱，及前驱节点的后继。
    if (root->lchild == NULL) {
        root->lchild = pre;
        root->ltag = THREAD;
    }
    if (pre && !pre->rchild) {
        pre->rchild = root;
        pre->rtag = THREAD;
    }
    pre = root;

    build_thread_tree(root->rchild);
}

Node *getLeftMost(Node *n) {
    while (n && n->ltag == CHILD && n->lchild)
        n = n->lchild;
    return n;
}

void output(Node *root) {
    if (!root) return;
    Node *n = getLeftMost(root);
    while (n) {
        printf("%d ", n->val);
        if (n->rtag == CHILD)
            n = getLeftMost(n->rchild);  // 非叶子节点，符合中序遍历
        else
            n = n->rchild; // 后继
    }
}

int main() {
    srand(time(NULL));
    Node *root = NULL;

    int cnt = 10;
    printf("Input         : ");
    while (cnt--) {
        int val = rand() % 100;
        printf("%d ", val);
        root = insert(root, val);
    }
    printf("\n");

    printf("Inorder output: ");
    inorder(root);
    printf("\n");

    printf("Thread output : ");
    build_thread_tree(root);
    output(root);
    printf("\n");

    freeTree(root);
    return 0;
}

图

一个图有很少边（如 \(e < n\log (n)\)，e 指边数，n 指点数）的图称为稀疏图，反之称为稠密图。

顶点的 度 是指依附于某个顶点的边数。

入度 是以该顶点为终点的弧的数目，出度 是以该顶点为起点的弧的数目。

稀疏图，一般用邻接表来存储，这样可以节省空间；如果是稠密图，一般用邻接矩阵来存储。

邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_N 500

typedef struct Graph {
    int mat[MAX_N][MAX_N];
    int n;
} Graph;

void init(Graph *g, int n) {
    g->n = n;
    memset(g->mat, 0, sizeof(g->mat));
}

void insert(Graph *g, int a, int x, int y) {
    if (x < 0 || x >= g->n || y < 0 || y >= g->n) {
        return ;
    }
    if (a) {
        g->mat[x][y] = 1;
        g->mat[y][x] = 1;
    } else {
        g->mat[x][y] = 1;
    }
}

void output(Graph *g) {
    for (int i = 0; i < g->n; ++i) {
        for (int j = 0; j < g->n; ++j) {
            (j) && printf(" ");
            printf("%d", g->mat[i][j]);
        }
        (i < g->n - 1) && printf("\n");
    }
}

int main() {
    int n, m, x, y;
    scanf("%d %d", &n, &m);
    Graph *graph = (Graph *)malloc(sizeof(Graph));
    init(graph, n);
    for (int i = 0; i < m; ++i) {
        scanf("%d %d", &x, &y);
        insert(graph, x, y);
    }
    output(graph);
    free(graph);
    return 0;
}

邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_N 10000

typedef struct Node {
    int vertex;
    struct Node *next;
} Node, *LinkedList;

LinkedList insert_node(LinkedList head, int index) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->vertex = index;
    node->next = head;
    head = node;
    return head;
}

typedef struct Graph {
    int n;
    LinkedList edges[MAX_N];
} Graph;

void init(Graph *g, int n) {
    g->n = n;
    for (int i = 0; i < g->n; ++i) {
        g->edges[i] = NULL;
    }
}

void insert(Graph *g, int a, int x, int y) {
    if (x < 0 || x >= g->n || y < 0 || y >= g->n) {
        return ;
    }
    if (a) {
        g->edges[x] = insert_node(g->edges[x], y);
        g->edges[y] = insert_node(g->edges[y], x);
    } else {
        g->edges[x] = insert_node(g->edges[x], y);
    }
}

void output(Graph *g) {
    for (int i = 0; i < g->n; ++i) {
        printf("%d:", i);
        for (Node *j = g->edges[i]; j != NULL; j = j->next) {
            printf(" %d", j->vertex);
        }
        (i < g->n - 1) && printf("\n");
    }
}

void clear(Graph *g) {
    for (int i = 0; i < g->n; ++i) {
        Node *head = g->edges[i];
        while (head != NULL) {
            Node *delete_node = head;
            head = head->next;
            free(delete_node);
        }
    }
    free(g);
}

int main() {
    int n, m, a, x, y;
    scanf("%d %d", &n, &m);
    Graph *graph = (Graph *)malloc(sizeof(Graph));
    init(graph, n);
    for (int i = 0; i < m; ++i) {
        scanf("%d %d %d", &a, &x, &y);
        insert(graph, a, x, y);
    }
    output(graph);
    clear(graph);
    return 0;
}

图搜索

深度优先

从开始节点，遍历相邻节点，若该节点没有被访问过，递归遍历其相邻节点。遇到没有遍历的，就向下递归。

利用邻接表实现DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_N 10000

typedef struct Node {
    int vertex;
    struct Node *next;
}Node, *LinkedList;

LinkedList insert_node(LinkedList head, int index) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->vertex = index;
    node->next = head;
    head = node;
    return head;
}

typedef struct Graph {
    LinkedList edges[MAX_N];
    int n;
    int visited[MAX_N];
}Graph;

void init(Graph *g, int n) {
    g->n = n;
    for (int i = 0; i < g->n; ++i) {
        g->edges[i] = NULL;
    }
    memset(g->visited, 0, sizeof(g->visited));
}

void insert(Graph *g, int x, int y) {
    if (x < 0 || x >= g->n || y < 0 || y >= g->n) {
        return ;
    }
    g->edges[x] = insert_node(g->edges[x], y);
    g->edges[y] = insert_node(g->edges[y], x);
}

void clear(Graph *g) {
    for (int i = 0; i < g->n; ++i) {
        Node *head = g->edges[i];
        while (head != NULL) {
            Node *delete_node = head;
            head = head->next;
            free(delete_node);
        }
    }
    free(g);
}

void dfs(Graph *g, int vertex) {
    printf("%d\n", vertex);
    g->visited[vertex] = 1;
    for (Node *adj = g->edges[vertex]; adj != NULL; adj = adj->next) {
        if (!g->visited[adj->vertex]) {
            dfs(g, adj->vertex);
        }
    }
}

int main() {
    int n, m, k;
    scanf("%d %d", &n, &m);
    Graph *graph = (Graph *)malloc(sizeof(Graph));
    init(graph, n);
    for (int i = 0; i < m; ++i) {
        int x, y;
        scanf("%d %d", &x, &y);
        insert(graph, x, y);
    }
    scanf("%d", &k);
    dfs(graph, k);
    clear(graph);
    return 0;
}

广度优先

先遍历完一个节点的所有相邻节点，再遍历相邻节点的相邻节点。

使用 queue 实现广度优先搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_N 10000

typedef struct Queue {
    int *data;
    int head, tail, length;
} Queue;

void init_queue(Queue *q, int length_input) {
    q->data = (int *)malloc(sizeof(int) * length_input);
    q->length = length_input;
    q->head = 0;
    q->tail = -1;
}

void push(Queue *q, int element) {
    if (q->tail + 1 < q->length) {
        q->tail++;
        q->data[q->tail] = element;
    }
}

int front(Queue *q) {
    return q->data[q->head];
}

void pop(Queue *q) {
    q->head++;
}

int empty(Queue *q) {
    if (q->head > q->tail) {
        return 1;
    } else {
        return 0;
    }
}

void clear_queue(Queue *q) {
    free(q->data);
    free(q);
}

typedef struct Node {
    int vertex;
    struct Node *next;
}Node, *LinkedList;

LinkedList insert_node(LinkedList head, int index) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->vertex = index;
    node->next = head;
    head = node;
    return head;
}

typedef struct Graph {
    LinkedList edges[MAX_N];
    int visited[MAX_N];
    int n;
}Graph;

void init_graph(Graph *g, int n) {
    g->n = n;
    memset(g->visited, 0, sizeof(g->visited));
    for (int i = 0; i < g->n; ++i) {
        g->edges[i] = NULL;
    }
}

void insert(Graph *g, int x, int y) {
    if (x < 0 || x >= g->n || y < 0 || y >= g->n) {
        return ;
    }
    g->edges[x] = insert_node(g->edges[x], y);
    g->edges[y] = insert_node(g->edges[y], x);
}

void clear_graph(Graph *g) {
    for (int i = 0; i < g->n; ++i) {
        Node *head = g->edges[i];
        while (head != NULL) {
            Node *delete_node = head;
            head = head->next;
            free(delete_node);
        }
    }
    free(g);
}

void bfs(Graph *g, int start_vertex) {
    Queue *queue = (Queue *)malloc(sizeof(Queue));
    init_queue(queue, g->n);
    push(queue, start_vertex);
    g->visited[start_vertex] = 1;
    while (!empty(queue)) {
        int vertex = front(queue);
        printf("%d\n", vertex);
        pop(queue);
        for (Node *adj = g->edges[vertex]; adj != NULL; adj = adj->next) {
            if (!g->visited[adj->vertex]) {
                g->visited[adj->vertex] = 1;
                push(queue, adj->vertex);
            }
        }
    }
    clear_queue(queue);
}

int main() {
    int n, m, k;
    scanf("%d %d", &n, &m);
    Graph *graph = (Graph *)malloc(sizeof(Graph));
    init_graph(graph, n);
    for (int i = 0; i < m; ++i) {
        int x, y;
        scanf("%d %d", &x, &y);
        insert(graph, x, y);
    }
    scanf("%d", &k);
    bfs(graph, k);
    clear_graph(graph);
    return 0;
}
Notes Data Structure
data structure cs basic

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！