数据结构整理-part3

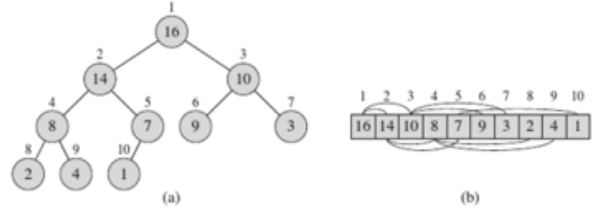
堆与优先队列

堆可以看成是一棵完全二叉树，除最后一层以外，它的每一层都是填满的，最后一层从左到右依次填入。

根结点权值大于等于树中任意结点权值的堆称为大根堆。

根结点权值小于等于树中任意结点权值的堆则称为小根堆。

并不需要真的维护一棵完全二叉树，而只需用一个数组来存储，堆按从上到下，从左到右的顺序，依次存储在下标从 1 开始的数组里。

元素插入，先添加到完全二叉树的最后一位之后，然后对比与父节点的关系，判断是否交换与父节点的位置。

元素删除，先对调堆顶元素与完全二叉树最后一个元素，删除最后一个元素，然后从堆顶开始调整二叉树的堆序性。

堆排序，和元素删除类似，只是不删除对调之后的最后一个元素，只是将序列尾部 index 减一。直到 index 等于 0。

总而言之，挺简单的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <stdio.h>
#include <stdlib.h>

typedef struct Heap {
    int *data, size;
} Heap;

void init(Heap *h, int length_input) {
    h->data = (int *)malloc(sizeof(int) * length_input);
    h->size = 0;
}

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void push(Heap *h, int value) {
    h->data[h->size] = value;
    int cur = h->size;
    int parent = (cur - 1) / 2;
    while (h->data[cur] > h->data[parent]) {
        swap(&h->data[cur], &h->data[parent]);
        cur = parent;
        parent = (cur - 1) / 2;
    }
    h->size++;
}

void output(Heap *h) {
    for (int i = 0; i < h->size; i++) {
        (i > 0) && printf(" ");
        printf("%d ", h->data[i]);
    }
    printf("\n");
}

int top(Heap *h) {
    return h->data[0];
}

void update(Heap *h, int pos, int n) {
    int lchild = 2 * pos + 1, rchild = 2 * pos + 2;
    int max_idx = pos;
    if (h->data[lchild] > h->data[max_idx] && lchild < n)
        max_idx = lchild;
    if (rchild < n && h->data[rchild] > h->data[max_idx])
        max_idx = rchild;
    if (max_idx != pos) {
        swap(&h->data[max_idx], &h->data[pos]);
        update(h, max_idx, n);
    }
    return;
}

void pop(Heap *h) {
    swap(&h->data[0], &h->data[--h->size]);
    update(h, 0, h->size);
}

void heap_sort(Heap *h) {
    for (int i = h->size - 1; i > 0; i--) {
        swap(&h->data[i], &h->data[0]);
        update(h, 0, i);
    }
}

void clear(Heap *h) {
    free(h->data);
    free(h);
}

int main() {
    Heap *h = (Heap *)malloc(sizeof(Heap));
    init(h, 105);

    int n;
    scanf("%d", &n);
    for (int i = 0, val; i < n; i++) {
        scanf("%d", &val);
        push(h, val);
    }

    int m;
    scanf("%d", &m);
    while (m--) {
        printf("%d\n", top(h));
        pop(h);
    }
    output(h);

    heap_sort(h);
    output(h);

    clear(h);
    return 0;
}

优先队列

在 C++ 的 STL 里，有封装好的优先队列priority_queue，它包含在头文件<queue>里。优先级可以自己定义，默认优先级是权值大的元素优先级高。

字符串Huffman编码

建立Huffman树的方法，在总结 树 的部分有说明。

首先统计每个字母在字符串里出现的频率，把每个字母看成一个结点，结点的权值即是字母出现的频率。

把每个结点看成一棵只有根结点的二叉树，一开始把所有二叉树（结点）都放在一个集合里，接下来开始如下编码：

步骤一：从集合里取出两个根结点权值最小的树a和b，构造出一棵新的二叉树c，二叉树c的根结点的权值为a和b的根结点权值和，二叉树c的左右子树分别是a和b。（合并）

步骤二：将二叉树a和b从集合里删除，把二叉树c加入集合里。（更新候选）

重复以上两个步骤，直到集合里只剩下一棵二叉树，最后剩下的就是哈夫曼树了。

规定每个有孩子的结点，到左孩子的路径为 0，到右孩子的路径为 1。每个字母的编码就是根结点到字母对应结点的路径。

计算字符串进行哈夫曼编码后的长度，即哈夫曼树的带权路径长度 WPL（Weighted Path Length），也就是每个叶子结点到根结点的距离乘以叶子结点权值结果之和。

一种简单的计算方法是：当哈夫曼树上结点总个数大于 1 时，哈夫曼树的 WPL，等于树上除根结点之外的所有结点的权值之和。如果结点总个数为 1，则哈夫曼树的 WPL 即为根结点权值。

想想Huffman树建立的过程，这种简单的计算WPL的方法，挺直观的。

利用小根堆计算Huffman树的WPL

不考虑建立二叉树的步骤，只累加计算每次作为插入结点的权值之和就能得到结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <stdio.h>
#include <stdlib.h>

typedef struct Heap {
    int *data, size;
} Heap;

void init(Heap *h, int length_input) {
    h->data = (int *)malloc(sizeof(int) * length_input);
    h->size = 0;
}

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void push(Heap *h, int value) {
    h->data[h->size] = value;
    int current = h->size;
    int father = (current - 1) / 2;
    while (h->data[current] < h->data[father]) {
        swap(&h->data[current], &h->data[father]);
        current = father;
        father = (current - 1) / 2;
    }
    h->size++;
}

int top(Heap *h) {
     return h->data[0];
}

void update(Heap *h, int pos, int n) {
    int lchild = 2 * pos + 1, rchild = 2 * pos + 2;
    int max_value = pos;
    if (lchild < n && h->data[lchild] < h->data[max_value]) {
        max_value = lchild;
    }
    if (rchild < n && h->data[rchild] < h->data[max_value]) {
        max_value = rchild;
    }
    if (max_value != pos) {
        swap(&h->data[pos], &h->data[max_value]);
        update(h, max_value, n);
    }
}

void pop(Heap *h) {
    swap(&h->data[0], &h->data[h->size - 1]);
    h->size--;
    update(h, 0, h->size);
}

int heap_size(Heap *h) {
    return h->size;
}

void clear(Heap *h) {
    free(h->data);
    free(h);
}

int main() {
    int n, value, ans = 0;
    scanf("%d", &n);
    Heap *heap = (Heap *)malloc(sizeof(Heap));
    init(heap, n);
    
    for (int i = 1; i <= n; i++) {
        scanf("%d", &value);
        push(heap, value);
    }
    
    if (n == 1) {
        ans = ans + top(heap);
    }
    while (heap_size(heap) > 1) {
        int a = top(heap);
        pop(heap);
        int b = top(heap);
        pop(heap);
        ans = ans + a + b;
        push(heap, a + b);
    }
    
    printf("%d\n", ans);
    
    clear(heap);
    return 0;
}

并查集

在数据结构里，森林是指若干棵互不相交的树的集合。

并查集（Merge-Find Set），也被称为不相交集合（Disjoint Set），是用于解决若干的不相交集合检索关系的数据结构。

一般并查集有以下几种操作：

  1. MAKE-SET(x)：初始化操作，建立一个只包含元素 x 的集合。
  2. UNION(x, y)：合并操作，将包含 x 和 y 的集合合并为一个新的集合。
  3. FIND-SET(x)：查询操作，计算 x 所在的集合。

“并查集”这个词通常既可以指代不相交集合的数据结构，也可以表示其对应的算法。其在有些教材中的英文名称也叫做 Disjoint Set Union，表示用于求不相交集合并集的相关算法。

并查集用有根树来表示集合，树中的每一个结点都对应集合的一个成员，每棵树表示一个集合。

每个成员都有一条指向父结点的边，整个有根树通过这些指向父结点的边来维护。

每棵树的根就是这个集合的代表，并且根的父结点是它自己。

并查集的查询操作，指的是查找出指定元素所在有根树的根结点是谁。

并查集的合并操作需要用到查询操作的结果。合并两个元素所在的集合，需要首先求出两个元素所在集合的根。接下来将其中一个根结点的父亲设置为另一个根结点。

优化方法

并查集的查询操作最坏情况下的时间复杂度为 \(O(n)\) 退化成一个单链表。

其优化方法是，在合并时，将高度较低的树接到高度较高的树根上，可以防止树退化成一条链。

  1. 利用一个数组保存每个节点的所在树的节点总数，即保存每个节点的秩（可视为height）。
  2. 分别获得传入的两个节点所在的树的根节点。
  3. 比较两个根节点是否，相同则返回 false，结束合并操作、
  4. 若两个根节点的秩不同，比较他们的秩的大小。
  5. 将秩较小的根节点的父指针指向秩较大的跟节点。
  6. 更新合并后的根节点的秩，返回 true，结束合并操作。

通过路径压缩的方法可以进一步减少均摊复杂度，此时同一个集合内的节点可以一步找到根节点。同时使用这两种优化方法，可以将每次操作的时间复杂度优化至接近常数级。

路径压缩指，在进行路径压缩优化时只需在查找根节点时，将待查找的节点的父指针指向它所在的树的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdlib.h>

typedef struct DisjointSet{
    int *father, *rank;
} DisjointSet;

void init(DisjointSet *s, int size) {
    s->father = (int *)malloc(sizeof(int) * size);
    s->rank = (int *)malloc(sizeof(int) * size);
    for (int i = 0; i < size; ++i) {
        s->father[i] = i;
        s->rank[i] = 1;
    }
}

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

int max(int a, int b) {
    return a > b ? a : b;
}

int find_set(DisjointSet *s, int node) {
    if (s->father[node] != node) {
        // 递归找到根节点，node的father指向根节点
        s->father[node] = find_set(s, s->father[node]);
    }
    // 回溯过程中，路径上node的father都指向根
    return s->father[node];
}

// 根据高度合并
int merge(DisjointSet *s, int node1, int node2) {
    int ancestor1 = find_set(s, node1);
    int ancestor2 = find_set(s, node2);
    if (ancestor1 != ancestor2) {
        if (s->rank[ancestor1] > s->rank[ancestor2]) {
            swap(&ancestor1, &ancestor2);
        }
        s->father[ancestor1] = ancestor2;
        s->rank[ancestor2] = max(s->rank[ancestor2], s->rank[ancestor1] + 1);
        return 1;
    }
    return 0;
}

void clear(DisjointSet *s) {
    free(s->father);
    free(s->rank);
    free(s);
}

int main() {
    DisjointSet *dsu = (DisjointSet *)malloc(sizeof(DisjointSet));
    init(dsu, 100);
    int m, x, y;
    scanf("%d", &m);
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &x, &y);
        int ans = merge(dsu, x, y);
        if (ans) {
            printf("success\n");
        } else {
            printf("failed\n");
        }
    }
    clear(dsu);
    return 0;
}

连通分量

连通分量就是图 G 的最大连通子图。对于一个无向图，使用FloodFill算法可以求得连通分量。

  1. 找到一个没有染色的顶点，将其染为新的颜色 \(Color_{new}\)，如果没有则算法结束。
  2. 初始化一个空的队列，并将第一步的顶点插入队列。
  3. 不断获得队首元素的值并弹出，将和队首元素相邻的未染色顶点染为 \(Color_{new}\)，并将其加入队列。
  4. 重复执行第一步，直到所有顶点都被染色，算法结束。

FloodFill 的时间复杂度是 \(O(V+E)\)，其中广度优先遍历的部分可以替换成深度优先遍历，复杂度是一样的。通常考虑到递归调用的时间开销，往往广度优先遍历的效率要更高一些。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <stdio.h>
#include <stdlib.h>

#define MAX_N 1000

typedef struct Graph {
    int n;
    int color[MAX_N];
    int mat[MAX_N][MAX_N];
} Graph;

void init_Graph(Graph *g, int input_n) {
    g->n = input_n;
    for (int i = 0; i < g->n; i++) {
        g->color[i] = 0;
        for (int j = 0; j < g->n; j++) {
            g->mat[i][j] = 0;
        }
    }
}

void insert(Graph *g, int x, int y) {
    g->mat[x][y] = 1;
    g->mat[y][x] = 1;
}

void floodfill(Graph *g) {
    int color_cnt = 0;
    int q[MAX_N];
    for (int i = 0; i < g->n; ++i) {
        if (g->color[i] == 0) {
            color_cnt++;
            g->color[i] = color_cnt;
            int l = 0, r = 0;
            q[r++] = i;
            // 遍历相邻未染色节点，通过队列，广度优先染色
            while (l < r) {
                int vertex = q[l++];
                for (int j = 0; j < g->n; j++) {
                    if (g->mat[vertex][j] && g->color[j] == 0) {
                        g->color[j] = color_cnt;
                        q[r++] = j;
                    }
                }
            }
        }
    }
    // output print
    for (int i = 0; i < g->n; ++i) {
        printf("%d %d\n", i, g->color[i]);
    }
}

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    Graph *g = (Graph *)malloc(sizeof(Graph));
    init_Graph(g, n);
    for (int i = 0; i < m; i++) {
        int a, b;
        scanf("%d %d", &a, &b);
        insert(g, a, b);
    }
    floodfill(g);
    free(g);
    return 0;
}

最小生成树

从一个带权图中抽出一棵生成树，使得边权值和最小，这棵生成树就叫做最小生成树。

Prim

思路很简单，不断寻找距离当前生成树最近的顶点。逐步添加最短边到生成树中。

定义带权图 G 的顶点集合为 V，接着再定义最小生成树的顶点集合为 U，初始集合 U 为空。

  1. 任选一个顶点 \(x\)，加入集合 \(U\)，并记录每个顶点到当前最小生成树的最短距离。
  2. 选择一个距离当前最小生成树最近的，且不属于集合 \(U\) 的顶点 \(v\)（如果有多个顶点 \(v\)，任选其一），将顶点 \(v\) 加入集合 \(U\)，并更新所有与顶点 \(v\) 相连的顶点到当前最小生成树的最短距离记录。 3. 重复第二步操作，直至集合 \(U\) 等于集合 \(V\)。

贪心策略，意味着就很直白，没啥难的。

使用不同的数据结构实现，时间复杂度不同。

EXTRACT-MIN DECREASE-KEY Total
array O(V) O(1) \(O(V^2)\)
binary heap O(log V) O(log V) \(O(E \log V)\)
Fibonacci heap O(log V) O(1) \(O(E + V\log V)\)

对于稠密图，E达到 \(O(V^2)\) 级别，使用 Fibonacci heap 实现的Prim算法比较合适。

下面的实现，起始有点模糊，抽象了一个 dist 数组。需要到实现过程中才能准确反映出他的意义。一个抽象的解释是，第 i 个节点到当前生成树的最小距离（权值最小的那条边的值）。将生成树看作一个整体的话，dist 数组中的有效值就是与生成树相连的所有边的权值。

通过 dist 数组，找到下一个生成树节点。然后更新加入新节点之后，新的 dist 数组。挺抽象的，但是还好，过程很短。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <stdio.h>
#include <stdlib.h>

#define MAX_N 1000

const int INF = 0x3f3f3f3f;

typedef struct Graph {
    int n;
    int visited[MAX_N], dist[MAX_N];
    int mat[MAX_N][MAX_N];
}Graph;

void init(Graph *g, int input_n) {
    g->n = input_n;
    for (int i = 0; i < g->n; i++) {
        for (int j = 0; j < g->n; j++) {
            g->mat[i][j] = INF;
        }
    }
}

void insert(Graph *g, int x, int y, int weight) {
    g->mat[x][y] = weight;
    g->mat[y][x] = weight;
}

int prim(Graph *g, int v) {
    int total_weight = 0;
    for (int i = 0; i < g->n; ++i) {
        g->visited[i] = 0;
        g->dist[i] = INF;
    }
    g->dist[v] = 0;
    for (int i = 0; i < g->n; ++i) {
        int min_dist = INF, min_vertex;
        // 贪心搜索下一个生成树节点
        for (int j = 0; j < g->n; ++j) {
            if (!g->visited[j] && g->dist[j] < min_dist) {
                min_dist = g->dist[j];
                min_vertex = j;
            }
        }
        total_weight += min_dist;
        g->visited[min_vertex] = 1;
        
        // 新加入节点后，更新dist数组
        for (int j = 0; j < g->n; ++j) {
            if (!g->visited[j] && g->mat[min_vertex][j] < g->dist[j]) {
                g->dist[j] = g->mat[min_vertex][j];
            }
        }
    }
    return total_weight;
}

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    Graph *g = (Graph *)malloc(sizeof(Graph));
    init(g, n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d %d %d", &a, &b ,&c);
        insert(g, a, b, c);
    }
    printf("%d\n", prim(g, 0));
    free(g);
    return 0;
}

实现中很容易发现，存在很多不必要的遍历，每次遍历都是从 0 到 n，显然存在优化的空间，以后遇到再说。

Kruskal

定义带权图 G 的边集合为 E，接着再定义最小生成树的边集合为 T，初始集合 T 都为空。

  1. 首先，把图 \(G\) 看成一个有 \(n\) 棵树的森林，图上每个顶点对应一棵树。
  2. 接着，将边集合 \(E\) 的每条边，按权值从小到大进行排序，
  3. 依次遍历每条边 \(e = (u, v)\)，记顶点 \(u\) 所在的树为 \(T_u\)，顶点 \(v\) 所在的树为 \(T_v\)，如果 \(T_u\) 和 \(T_v\) 不是同一棵树，则将边 \(e\) 加入集合 \(T\)，并将两棵树 \(T_u\) 和 \(T_v\) 进行合并。

算法执行完毕后，集合 \(T\) 记录了最小生成树的所有边。

贪心策略，每次都会选择一条两个顶点不在同一棵树且权值最小的边加入集合。

算法包括所有边权值排序和遍历所有边合并树。整体时间复杂度主要看排序部分 \(O(E\log(E))\)。所以对于结点多但是边少的稀疏图，性能会比Prim算法好。

实现上，排序使用快速排序，合并验证使用并查集，。

最短路径

求一个起点到其余各个顶点的最短路径问题。

Dijkstra

定义带权图 G 所有顶点的集合为 V，接着再定义已确定最短路径的顶点集合为 U，初始集合 U 为空。

  1. 首先将起点 \(x\) 加入集合 \(U\)，并在数组 \(A\) 中记录起点 \(x\) 到各个点的最短路径（如果顶点到起点 \(x\) 有直接相连的边，则最短路径为边权值，否则为一个极大值）。
  2. 从数组 \(A\) 中选择一个距离起点 \(x\) 最近的，且不属于集合 \(U\) 的顶点 \(v\)（如果有多个顶点 \(v\)，任选其一即可），将顶点 \(v\) 加入集合 \(U\)，并更新所有与顶点 \(v\) 相连的顶点到起点 \(x\) 的最短路径。
  3. 重复第二步操作，直至集合 \(U\) 等于集合 \(V\)。

算法结束，数组 \(A\) 记录了起点 \(x\) 到其余 \(n - 1\) 个点的最短路径。

和Prim很类似，差别在于比较大小的目标是距离起点 x 的距离。同时算法不能处理有负权边的问题（这是Bellman Ford这类算法解决的问题）。

时间复杂度和Prim类似，在是使用 Fibonacci heap 优化后，为\(O(E + V\log V)\)。

算法的关键就是更新当前最优结点的相邻结点的最短路径。（真的不喜欢贪心这个词，每次找到最值怎么就贪心了？贪心是已经得到最好，但是还是不满足的。）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
#include <stdlib.h>

#define MAX_N 1000

const int INF = 0x3f3f3f3f;

typedef struct Graph {
    int n;
    int visited[MAX_N], dist[MAX_N];
    int mat[MAX_N][MAX_N];
}Graph;

void init(Graph *g, int input_n) {
    g->n = input_n;
    for (int i = 0; i < g->n; ++i) {
        for (int j = 0; j < g->n; j++) {
            g->mat[i][j] = INF;
        }
    }
}

void insert(Graph *g, int x, int y, int weight) {
    g->mat[x][y] = weight;
    g->mat[y][x] = weight;
}

void dijkstra(Graph *g, int v) {
    for (int i = 0; i < g->n; ++i) {
        g->visited[i] = 0;
        g->dist[i] = INF;
    }
    g->dist[v] = 0;

    for (int i = 0; i < g->n; ++i) {
        int min_d = INF, min_i;
        // i结点当前到起点的最短路径
        for (int j = 0; j < g->n; ++j) {
            if (!g->visited[j] && g->dist[j] < min_d) {
                min_d = g->dist[j];
                min_i = j;
            }         
        }
        g->visited[min_i] = 1;
		// 从已知最短路径的结点开始，计算相邻结点到起点的最短路径是否需要更新
        for (int k = 0; k < g->n; k++) {
            if (!g->visited[k] && g->mat[min_i][k] + min_d < g->dist[k]) {
                g->dist[k] = g->mat[min_i][k] + min_d;
            }
        }
    }
}

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    Graph *g = (Graph *)malloc(sizeof(Graph));
    init(g, n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d %d %d", &a, &b ,&c);
        insert(g, a, b, c);
    }

    int v;
    scanf("%d", &v);

    dijkstra(g, v);
    for (int i = 0; i < n; i++) {
        printf("%d: %d\n", i, g->dist[i]);
    }
    free(g);
    return 0;
}

字符串匹配

这部分之前整理过，字符串匹配从KMP到AC自动机。但是这个东西就是容易忘。

基础的暴力搜索方法就不谈了，没啥可记的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stdio.h>
#include <string.h>

#define MAXLEN 1024

int match(char *buffer, char *pattern) {
    for (int i = 0; i < strlen(buffer) - strlen(pattern) + 1; ++i) {
        int j = 0;
        for (; j < strlen(pattern); ++j) {
            if (buffer[i + j] != pattern[j]) {
                break;
            }
        }
        if (j == strlen(pattern)) {
            return i;
        }
    }
    return -1;
}

int main() {
    char buffer[MAXLEN], pattern[MAXLEN];
    scanf("%s%s", buffer, pattern);
    int location = match(buffer, pattern);
    if (location != -1) {
        printf("match success, location is %d\n", location);
    } else {
        printf("match failed!\n");
    }
    return 0;
}

注意 i < strlen(buffer) - strlen(pattern) + 1，其中 + 1 才表示最后一段 pattern 长度的字符的起点index。

KMP

1
2
S: aaaaaababaaaaa
W: ababc

上例，abab匹配，c不匹配。暴力搜索会直接退回4个位置，从S中a的下一个b开始重新匹配W。

KMP的思想就是，不回退4，而是利用已经匹配过的字符，找到可以直接跳过，并且一定和W的一部分匹配的位置。比如上例中，第一次abab匹配，c不匹配，那么此时，根据W的规律，S中必然出现了abab。此时可以跳过S中a之后的第一个b，从第二个ab之后的位置开始匹配W的第一个ab之后的部分。

KMP就是分析W的规律，找到当每一个位置字符出现不匹配时，下一次匹配可以高效跳过的部分。

建立一个 Next 数组，记录在 W 中，拥有相同前缀的子串中最后一个字符的index值。就是下一次匹配开始的位置。注意其中一个子串是从 W 的第一个字符开始的，另一个字串位于 W 中间部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <string.h>

#define MAX_LEN 100010

void get_next(char *pat, int *next) {
    next[0] = 0;
    for (int i = 1, j = 0; i < strlen(pat); ++i) {
        // j - 1 代表已经成功匹配的最后一个位置的index，j为待匹配的第一个位置
        while (j && pat[j] != pat[i]) {
            j = next[j - 1];
        }
        if (pat[j] == pat[i]) {
            j++;
        }
        next[i] = j;
    }
}

int find(char *buffer, char *pat, int *next) {
    // j 代表j - 1 及之前的部分已经匹配，匹配成功会等于 pat 的长度
    for (int i = 0, j = 0; i < strlen(buffer); ++i) {
        while (j && pat[j] != buffer[i]) {
            j = next[j - 1];
        }
        if (pat[j] == buffer[i]) {
            j++;
        }
        if (j == strlen(pat)) {
            return i - j + 1;
        }
    }
    return -1;
}

int main() {
    char buffer[MAX_LEN], pattern[MAX_LEN];
    int next[MAX_LEN];
    scanf("%s%s", buffer, pattern);
    get_next(pattern, next);
    int location = find(buffer, pattern, next);
    
    if (location == -1) {
        printf("No\n");
    } else {
        printf("Yes\n%d\n", location);
    }
    
    return 0;
}

Trie

多个模式字符串前缀树，处理一个输入串从多个模式字符串中进行匹配前缀的情况。

Trie 树有以下特点：

  1. Trie 树的根结点上不存储字符，其余结点上存且只存一个字符。
  2. 从根结点出发，到某一结点上经过的字符，即是该结点对应的前缀。
  3. 每个结点的孩子结点存储的字符各不相同。
  4. Trie 树牺牲空间来换取时间，当数据量很大时，会占用很大空间。如果字符串均由小写字母组成，则每个结点最多会有 \(26\) 个孩子结点，则最多会有 \(26^n\) 个用于存储的结点，\(n\) 为字符串的最大长度。

Trie 树常用于字符串的快速检索，字符串的快速排序与去重，文本的词频统计等。查询效率对于长度为 n 的输入串，时间复杂为 O(n)。

下面程序利用Trie计算一段输入串 S 中不重复的字串个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

const int N = 100010;
const int SIZE = 26;
const char BASE = 'a';

typedef struct TrieNode {
    int is_terminal;
    struct TrieNode **childs; // 26个字母
} TrieNode, *Trie;


TrieNode* new_node() {
    Trie p = (Trie)malloc(sizeof(TrieNode));
    p->childs = (Trie *)malloc(sizeof(Trie) *SIZE);
    for (int i = 0; i < SIZE; i++) {
        p->childs[i] = NULL;
    }
    p->is_terminal = 0;
    return p;
}

void clear(Trie t) {
    if (t) {
        for (int i = 0; i < SIZE; ++i) {
            if (t->childs[i]) {
                clear(t->childs[i]);
            }
        }
        free(t->childs);
        free(t);
    }
}

// 增肌一个参数 res，累计一段字符串中不同字串的个数。
void insert(Trie trie, char *pattern, int *res) {
    TrieNode *p = trie;
    for (int i = 0; i < strlen(pattern); ++i) {
        if (p->childs[pattern[i] - BASE] == NULL) {
            p->childs[pattern[i] - BASE] = new_node();
            (*res)++;
        }
        p = p->childs[pattern[i] - BASE];
    }
    p->is_terminal = 1;
}

int find(Trie trie, char *buffer) {
    TrieNode *p = trie;
    for (int i = 0; i < strlen(buffer); i++) {
        if (p->childs[buffer[i] - BASE] == NULL) {
            return 0;
        }
        p = p->childs[buffer[i] - BASE];
    }
    return p->is_terminal;
}

int main() {
    char s[100005];
    scanf("%s", s);
	
    // 计算累计一段字符串中不同字串的个数。
    int res = 0;
    Trie root = new_node();
    for (int i = 0; i < strlen(s); ++i) {
        insert(root, s + i, &res);
    }

    printf("%d", res);

    clear(root);
    return 0;
}

AC自动机

处理多个模式串，在一个输入串 S 中搜索出现的模式串的问题。

AC自动机约等于Trie + KMP，加速多pattern匹配过程。

  1. 构建 patterns 的 Trie
  2. 构建 fail 指针
  3. 开始匹配

构建 fail 指针

  1. 在Trie中，BFS遍历，第一层，fail指针都指向 root
  2. 第一层之后，每个节点的 fail 指针，指向 【该节点的父节点】 的 【fail指针指向的节点】 的 【儿子节点】中 【和该节点（自己）同字符的节点】。如果没有找到，【fail指针指向的节点】继续向上找 fail 节点，直到 root。

fail指针表示的是以当前字符作为开头的最长后缀所在的位置。

匹配过程

  1. 输入string s，trie从 root开始，进行匹配
  2. 当匹配失败，跳转到fail指针指向的节点，如果fail到 root，输入此位置之后的string s的部分，继续查找。
  3. 当匹配成功（Trie标记的节点），也跳转到fail指针指向的节点，如果此时跳转到 root，进行回溯到前一个最长的trie路径节点。

下面的程序，输入一个字符串，输出输入串中出现多少个已知pattern。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

const int SIZE = 26;
const char BASE = 'a';
const int MAX_SIZE = 20005;
const int MAX_LEN = 25;

typedef struct TrieNode {
    int count;
    struct TrieNode** childs;
    struct TrieNode* fail;
} TrieNode, *Trie;

TrieNode* new_node() {
    TrieNode *p = (TrieNode *)malloc(sizeof(TrieNode));
    p->childs = (TrieNode **)malloc(sizeof(TrieNode *) * SIZE);
    for (int i = 0; i < SIZE; i++) {
        p->childs[i] = NULL;
    }
    p->fail = NULL;
    p->count = 0;
    return p;
}

void clear(TrieNode *p) {
    if (p != NULL) {
        for (int i = 0; i < SIZE; i++) {
            if (p->childs[i] != NULL) {
                clear(p->childs[i]);
            }
        }
        free(p->childs);
        free(p);
    }
}

// 构建Trie，并记录每个pattern出现次数，保存在每个node的count属性中
void insert(Trie trie, char *buffer) {
    TrieNode *p = trie;
    for (int i = 0; i < strlen(buffer); i++) {
        if (p->childs[buffer[i] - BASE] == NULL) {
            p->childs[buffer[i] - BASE] = new_node();
        }
        p = p->childs[buffer[i] - BASE];
    }
    p->count++;
}

// 构建fail指针
void build_automaton(Trie root) {
    root->fail = root;
    TrieNode *q[MAX_SIZE]; // 这里的BFS使用数组模拟queue
    int l = 0, r = 0;
    q[r++] = root;
    // BFS
    while (l < r) {
        TrieNode *now = q[l++];
        for (int i = 0; i < SIZE; ++i) {
            if (now->childs[i] != NULL) {
                TrieNode *child = now->childs[i];
                if (now == root) { // root指向自己
                    child->fail = root;
                } else {
                    TrieNode *iter = now;
                    // 找到fail指针中相同字符
                    while (iter != root && iter->fail->childs[i] == NULL) {
                        iter = iter->fail;
                    }
                    // 检查是否可以从fail指针的child开始向下匹配
                    if (iter->fail->childs[i] != NULL) {
                        child->fail = iter->fail->childs[i];
                    } else {
                        child->fail = root;
                    }
                }
                // BFS 每一层node
                q[r++] = child;
            }
        }
    }
}

int match_count(Trie root, const char *buffer) {
    TrieNode *p = root;
    int total_count = 0;
    for (int i = 0; buffer[i]; ++i) {
        // pattern不匹配，向fail指针回溯
        while (p != root && p->childs[buffer[i] - BASE] == NULL) {
            p = p->fail;
        }
        p = p->childs[buffer[i] - BASE];
        if (p == NULL) {
            p = root;
        }
        
        // 累加匹配成功的Trie树路径上，有效pattern的数量，因为回溯停止时，停在最大匹配处
        TrieNode *iter = p;
        while (iter != root) {
            total_count += iter->count;
            iter = iter->fail;
        }
    }
    return total_count;
}

int main() {
    Trie root = new_node();
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        char pattern[MAX_LEN];
        scanf("%s", pattern);
        insert(root, pattern);
    }
    build_automaton(root);
    char str_buffer[100005];
    scanf("%s", str_buffer);
    printf("%d\n", match_count(root, str_buffer));
    clear(root);
    return 0;
}
Notes Data Structure
data structure cs basic

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！