贝叶斯超参数搜索

paper by Bergstra et al

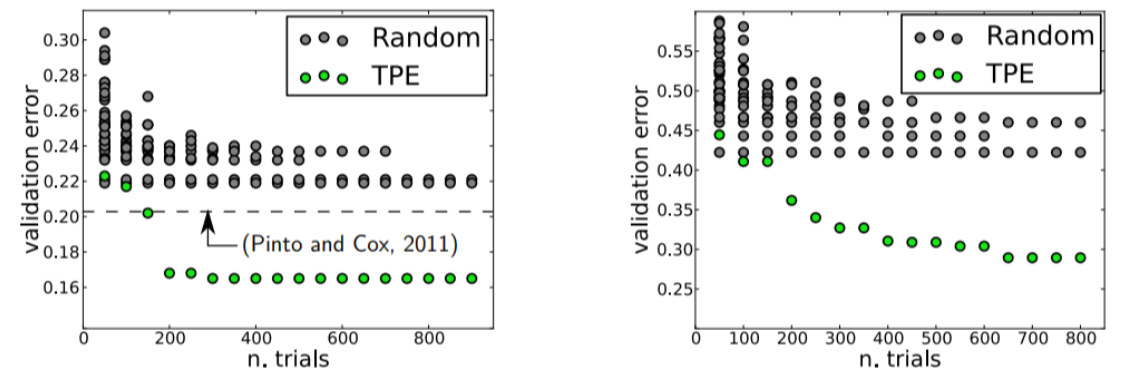
一句话概括Bayesian hyperparameter optimization：

build a probability model of the objective function and use it to select the most promising hyperparameters to evaluate in the true objective function.

常用算法：Sequential Model-Based Optimization (SMBO) with the Tree Parzen Estimator (TPE)

原理简述

贝叶斯方法相较于随机搜索和网格搜索，是更高效的。随机搜索和网格搜索根本不关注过去的结果，而是继续在整个范围内搜索，即使最优答案(可能)很明显在一个小区域内。

与随机或网格搜索相反，贝叶斯方法跟踪过去的评估结果，建立形成一个概率模型，将超参数映射到目标函数上得分的概率。这个模型被称为目标函数的代理。代理模型（也叫做响应面）又相对更容易优化。

运行过程为：

1. 建立目标函数的替代概率模型，代理模型

2. 查找在代理上性能最佳的超参数

3. 将这些超参数应用于真正的目标函数

4. 更新包含新结果的代理模型

5. 重复步骤2-4，直到达到最大迭代次数或时间为止

贝叶斯推理的目的是通过在每次评估目标函数后不断地更新概率模型，从而获得更多的数据，减少错误。

贝叶斯优化方法是有效的，因为它们有根据的选择了下一个超参数。 基本思想是：花更多的时间选择下一个超参数，以减少对目标函数的调用。 实际上，与在目标函数中花费的时间相比，选择下一个超参数所花费的时间是很少的。 通过评估从过去的结果看似更有希望的超参数，贝叶斯方法可以在更少的迭代中找到比随机搜索更好的模型设置。

一个简单的解释如下图：

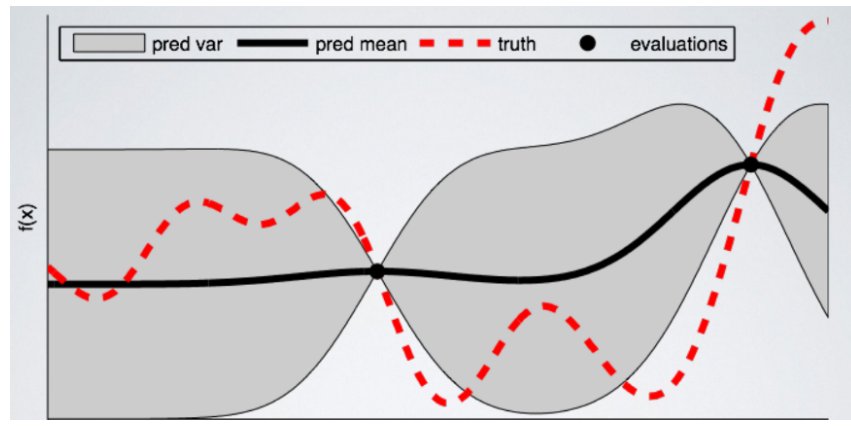
代理模型是粗黑线和器上线界细黑线组成的区域。红色虚线表示真实的目标函数。

经过贝叶斯优化几轮迭代之后，得到：

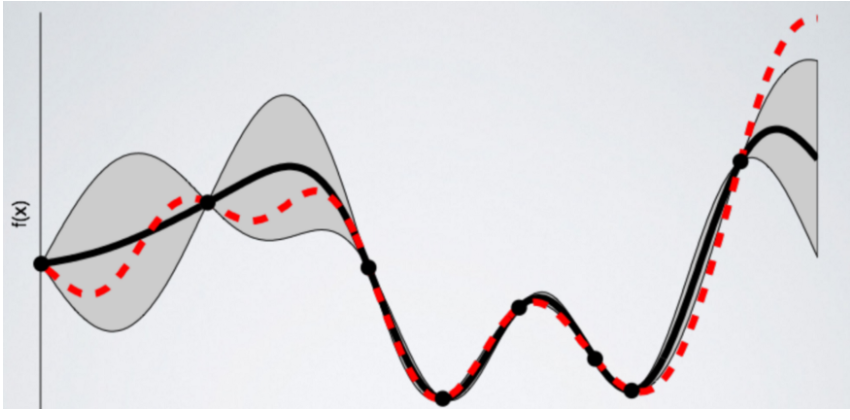
代理模型逐渐趋近目标函数。

Sequential Model-Based Optimization

Sequential是指一个接一个地进行试验，每次都通过应用贝叶斯推理更新概率模型(代理)来获取更好的超参数。组成部分有：

1. 要搜索的超参数域

2. 以超参数为输入并输出得分的目标函数

3. 目标函数的代理模型

4. 一个criteria（Selection Function），称为选择函数，用于评估从替代模型中下一步要选择的超参数

5. 该算法由（得分，超参数）对组成的历史记录，该历史对由算法用于更新代理模型

代理模型的选择有：Gaussian Processes, Random Forest Regressions, , Tree Parzen Estimators (TPE).

criteria常用Expected Improvement

代理模型，也称为响应面，是利用以前的评估结果建立的目标函数的概率表示。

Expected Improvement选择函数

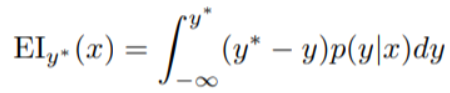
y* -- 目标函数的阈值

x -- 超参数组合的集合

y -- 输入x超参数得到的目标函数真实返回值

p(y | x) -- 代理模型输出的概率

其目的是最大化关于x的Expected Improvement。

如果p (y | x)在y < y*处，都为零，则超参数x不会产生任何改进。

如果积分为正，则意味着超参数x预期会产生比阈值更好的结果。

Tree-structured Parzen Estimator (TPE)

使用贝叶斯公式，计算p(y | x)

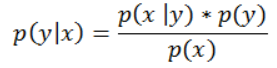
p (x | y)，是给定目标函数得分的超参数的概率。

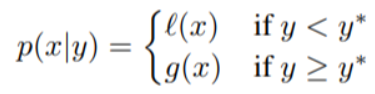
对超参数做了两种不同的分布:一种是目标函数的值小于阈值，l(x)，另一种是目标函数的值大于阈值，g(x)。

结合SMBO以及一点直观的印象，我们希望从l(x)而不是从g(x)中得出x的值，因为这种分布只基于产生低于阈值得分的x的值。

最终得到的Expected Improvement：

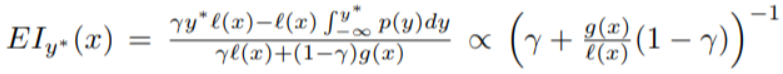
可以发现Expected Improvement和l(x) / g(x)的比值成反比。提高EI，正是需要从l(x)中多得到p (x | y)的值。

该算法利用历史得分建立l(x)和g(x)，提出目标函数的概率模型，代理模型随着每次迭代而改进。

工具

Spearmint， MOE ： Gaussian Process (surrogate)

Hyperopt ：Tree-structured Parzen Estimator Notebook示例，示例，示例

SMAC ：Random Forest regression.

都使用Expected Improvement选择函数。