回顾神经网络初始化方法
那么首先我们已经知道,全0或者常数、过大、过小的权重初始化都有梯度消失或者梯度爆炸的问题。而我们所期望的初始化状态是:期望为0,方差在一定范围内,同时尽量保证不同层的权重方差的一致性。这样出现internal covariance shift的可能性会大幅降低。闲来无事,适巧康康。
为了更简洁的期望与方差
首先需要知道期望\(E\)和方差\(Var\)的计算方法,基本公式: \[ Var(X)=E(X^2)-(E(X))^2 \]
\[ Covariance(X,Y)=E((X-E(X))(Y-E(Y)))\\ =E(XY)-E(X)E(Y) \]
当X,Y为独立的随机变量,Corvariance(即Cov)为0。
可以表示出两个独立随机变量的和的方差: \[ Var(X+Y)=E((X+Y)^2)-(E(X+Y))^2\\ =E(X^2+Y^2+2XY)-(E(X)+E(Y))^2\\ =E(X^2)-(E(X))^2+E(Y^2)-(E(Y))^2\\ =Var(X)+Var(Y) \] 两个独立随机变量的积的方差: \[ Var(XY)=E((XY)^2)-(E(XY))^2\\ =E(X^2)E(Y^2)-(E(X)E(Y))^2\\ =(Var(X)+E(X)^2)(Var(Y)+E(Y)^2)-(E(X)E(Y))^2\\ =Var(X)Var(Y)+E(X)^2Var(Y)+Var(X)E(Y)^2 \]
神经网络计算过程一般性表达
基本的计算方式: \[ Z_l=WA_{l-1}+B\\ A_l=f(Z_l) \] W与A是相互独立的。每一层不同神经元的权重\(w_i\)是独立同分布的。
假如W与A的分布已知,那么Z的方差可以计算: \[ Var(z)=Var(\sum_{i}^{fan\_in} w_ia_i)\\ =fan\_in \times (Var(w)Var(a)+E(w)^2Var(a)+Var(w)E(a)^2) \] fan_in表示输入单元个数,每个输入单元的激活值与对应的权重相乘求和,得到当前层的激活值。独立同分布,所以和的方差可以简化为方差之和。
不同激活函数的影响
初始化的目的始终是避免梯度爆炸或者消失,最好可以加快收敛速度。那么在分析整个网络的参数逐层变化时,需要分析一般性的变化规律。
激活值的分布,受到激活函数的形式影响,这是一个关键的因素。
对称型激活函数
tanh,sigmoid等关于x轴对称的函数,可以保证激活值的期望也为0。而此时,方差的计算得到简化: \[ Var(Z_l)=fan\_in^{l} \times \prod_{l=1}^{L}Var(w_l) \times Var(Z_{l-1}) \] 同时考虑反向传播的过程,其差异在于fan_in 变为 fan_out,详细过程见论文。同时约束前向和反向的系数都为1,那么,可以假设权重的分布为 \[ N(0, \frac{2}{fan\_in+fan\_out}) \] 若为均匀分布,可以假设 \[ U(-\frac{\sqrt{6}}{fan\_in+fan\_out}, \frac{\sqrt{6}}{fan\_in+fan\_out}) \]
非对称分段激活函数
ReLU这类激活函数,激活值的期望不再为0,公式(6)可以进行另一种变换。注意w的期望依然是我们所假设的0,这和激活值的分布是独立的。 \[ Var(z) =fan\_in \times (Var(w)Var(a)+E(w)^2Var(a)+Var(w)E(a)^2)\\ =fan\_in \times (Var(w)Var(a)+Var(w)E(a)^2)\\ =fan\_in \times (Var(w)[E(a^2)-E(a)^2]+Var(w)E(a)^2)\\ =fan\_in \times Var(w) \times E(a^2) \] 何凯明推出: \[ Var(Z_l)=\frac{1}{2} \times fan\_in \times Var(w_l) \times Var(Z_{l-1}) \] 假设两层之间系数为1,权重可假设为分布: \[ N(0, \frac{2}{fan\_in}) \] 如果按照反向传播计算: \[ N(0, \frac{2}{fan\_out}) \] 在caffe的实现中,可以选择使用 \[ N(0, \frac{4}{fan\_in + fan\_out}) \]
当然也可以不从激活函数入手,使用Normalization方法,强制变换分布。
来自神经网络训练动力学研究的一点点总结
神经网络学习过程,可以从信号频域角度分析。神经网络擅长并且优先学习低频信号信息,而不擅长学习高频振荡信号。也因此,通常模型的参数学习结果是一个比较平滑的曲面(该研究主要是在浅层网络上实验)。论文中说,如无必要,勿增频率。
报告中还展示了一种设计思路,以提高网络处理高频信号的能力,就是scale到较低的值域,以获得相对较小的参数空间。
而参数的初始化,不仅对参数的频率信息有影响,还影响着模型在不同条件下的收敛速度和收敛性(报告展示了浅层网络在MNIST实验的结果)。
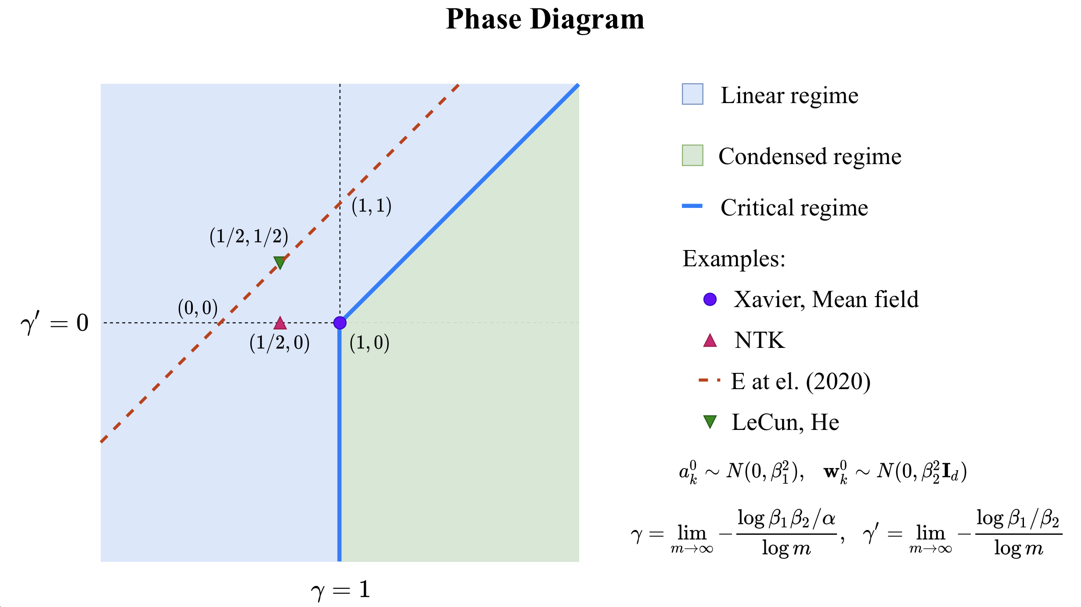
实验也指出了多种常用初始化在该理论中,都具有较好的性能。这里的变量和公式,比较复杂,这里也只关心了结论。
大模型训练后期,参数会偏向简化参数空间,向更少的方向聚集参数梯度向量,出现趋向相同方向的权重。
所以论文的结论为,神经网络存在这小网络偏好,如无必要,勿增神经元。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!