数据结构整理-part2

哈希表

将key的值通过一个设计好的hash函数转换，在连续内存地址上寻址找到对应的值。

hash函数构造方法：

  • 直接寻址法：将key值线性的映射到存储地址上。少量key适用。
  • 除留余数法：将key值对整数 p 取的余数直接做为存储地址。一般选择不大于 p 的最大质数。
  • 字符串hash的 BKD hash。
  • ...

hash函数设计要求计算简单，值尽量均匀分布。

冲突处理

开放地址法

如果发生冲突，那么就使用某种策略寻找下一存储地址，直到找到一个不冲突的地址或者找到关键字，否则一直按这种策略继续寻找。如果冲突次数达到了上限则终止程序，表示关键字不存在哈希表里。

  1. 线性探测法，如果当前的冲突位置为 \(d\)，那么接下来几个探测地址为 \(d + 1\)，\(d + 2\)，\(d + 3\) 等，也就是从冲突地址往后面一个一个探测；
  2. 线性补偿探测法，它形成的探测地址为 \(d + m\)，\(d + 2 \times m\)，\(d + 3 \times m\) 等，与线性探测法不同，这里的查找单位不是 \(1\)，而是 \(m\)，为了能遍历到哈希表里所有位置，设置 \(m\) 和表长 \(size\) 互质；
  3. 随机探测法，这种方法和前两种方法类似，这里的查找单位不是一个固定值，而是一个随机序列。
  4. 二次探测法，它形成的探测地址为 \(d + 1^2\)，\(d - 1^2\)，\(d + 2^2\)，\(d - 2^2\) 等，这种方法在冲突位置左右跳跃着寻找探测地址。

规定，当冲突次数小于表长的一半时，就可以把字符串插入到哈希表中。而如果发生冲突次数大于表长的一半时，就需要调用重建函数去重建哈希表了，因为认为哈希表已经发生了“堆聚”现象，这种情况下要扩大哈希表的容量，提高查找和插入的效率。

开放地址法计算简单快捷，处理起来方便，但是也存在不少缺点。

线性探测法容易形成“堆聚”的情况，即很多记录就连在一块，而且一旦形成“堆聚”，记录会越聚越多。

另外，开放地址法都有一个缺点，删除操作显得十分复杂，不能直接删除关键字所在的记录，否则在查找删除位置后面的元素时，可能会出现找不到的情况，因为删除位置上已经成了空地址，查找到这里时会终止查找。

链地址法

该方法将所有哈希地址相同的结点构成一个单链表，单链表的头结点存在哈希数组里。链地址法常出现在经常插入和删除的情况下。

相比开放地址法，链地址法有以下优点：不会出现“堆聚”现象，哈希地址不同的关键字不会发生冲突；不需要重建哈希表，在开放地址法中，如果哈希表里存满关键字了就需要扩充哈希表然后重建哈希表，而在链地址法里，因为结点都是动态申请的，所以不会出现哈希表里存满关键字的情况；相比开放地址法，关键字删除更方便，只需要找到指定结点，删除该结点即可。

当然代价就是查找效率会稍低一点，但是对于hash来讲这一点效率影响在大多数非极端条件下，使用体验基本没有啥区别。

当关键字规模少的时候，开放地址法比链地址法更节省空间，因为用链地址法可能会存在哈希数组出现大量空地址的情况，而在关键字规模大的情况下，链地址法就比开放地址法更节省空间，链表产生的指针域可以忽略不计，关键字多，哈希数组里产生的空地址就少了。

实现线性探测法hash

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct HashTable {
    char **elem;
    int size;
} HashTable;

void init(HashTable *h);
int hash(HashTable *h, char value[]);
int search(HashTable *h, char value[], int *pos, int *times);
int insert(HashTable *h, char value[]);
void recreate(HashTable *h);

void init(HashTable *h) {
    h->size = 2000;
    h->elem = (char **)malloc(sizeof(char *) * h->size);
    for (int i = 0; i < h->size; i++) {
        h->elem[i] = NULL;
    }
}

int hash(HashTable *h, char value[]) {
    int code = 0;
    for (size_t i = 0; i < strlen(value); i++) {
        code = (code * 256 + value[i] + 128) % h->size;
    }
    return code;
}

int search(HashTable *h, char value[], int *pos, int *times) {
    *pos = hash(h, value);
    *times = 0;
    while (h->elem[*pos] != NULL && strcmp(h->elem[*pos], value) != 0) {
        (*times)++;
        if (*times < h->size) {
            *pos = (*pos + 1) % h->size;
        } else {
            return 0;
        }
    }
    if (h->elem[*pos] != NULL && strcmp(h->elem[*pos], value) == 0) {
        return 1;
    } else {
        return 0;
    }
}

int insert(HashTable *h, char value[]) {
    int pos, times;
    // pos在search函数结束时时待插入元素的位置，times为冲突计数
    if (search(h, value, &pos, &times)) {
        return 2;
    } else if (times < h->size / 2) {
        h->elem[pos] = (char *)malloc(strlen(value) + 1);
        strcpy(h->elem[pos], value);
        return 1;
    } else {
        recreate(h);
        insert(h, value);
        return 0;
    }
}

// 当插入值的冲突数大于size的一半时，增大哈希表。
void recreate(HashTable *h) {
    // 获取原哈希表中元素
    char **temp_elem;
    temp_elem = (char **)malloc(sizeof(char *) * h->size);
    for (int i = 0; i < h->size; i++) {
        if (h->elem[i] != NULL) {
            temp_elem[i] = (char *)malloc(strlen(h->elem[i]) + 1);
            strcpy(temp_elem[i], h->elem[i]);
        } else {
            temp_elem[i] = NULL;
        }
    }
    // 释放原哈希表中元素
    for (int i = 0; i < h->size; i++) {
        if (h->elem[i] != NULL) {
            free(h->elem[i]);
        }
    }
    free(h->elem);
    
    // 创建新哈希表
    int copy_size = h->size;
    h->size = h->size * 2;
    h->elem = (char **)malloc(sizeof(char *) * h->size);
    for (int i = 0; i < h->size; i++) {
        h->elem[i] = NULL;
    }
    for (int i = 0; i < copy_size; i++) {
        if (temp_elem[i] != NULL) {
            insert(h, temp_elem[i]);
        }
    }
    
    // 释放内存
    for (int i = 0; i < copy_size; i++) {
        if (temp_elem[i] != NULL) {
            free(temp_elem[i]);
        }
    }
    free(temp_elem);
}

void clear(HashTable *h) {
    for (int i = 0; i < h->size; ++i) {
        if (h->elem[i] != NULL) {
            free(h->elem[i]);
        }
    }
    free(h->elem);
    free(h);
}

int main() {
    HashTable *hashtable = (HashTable*)malloc(sizeof(HashTable));
    init(hashtable);
    char buffer[1000];
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%s", buffer);
        int ans = insert(hashtable, buffer);
        if (ans == 0) {
            printf("recreate while insert!\n");
        } else if (ans == 1) {
            printf("insert success!\n");
        } else if (ans == 2) {
            printf("It already exists!\n");
        }
    }
    int temp_pos, temp_times;
    scanf("%s", buffer);
    if (search(hashtable, buffer, &temp_pos, &temp_times)) {
        printf("search success!\n");
    } else {
        printf("search failed!\n");
    }
    clear(hashtable);
    return 0;
}

实现链地址法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

typedef struct Node {
    char *str;
    struct Node *next;
} Node;

typedef struct HashTable {
    Node **data;
    int size;
} HashTable;

Node *initNode(const char *str) {
    Node *n = (Node *)malloc(sizeof(Node));

    //n->str = (char *)malloc(strlen(str) + 1);
    //strcpy(n->str, str);
    // 等价操作
    n->str = strdup(str);
    n->next = NULL;
    return n;
}

void freeNode(Node *n) {
    if (!n) return;
    free(n->str);
    free(n);
    return;
}

void freeList(Node *list) {
    if (!list) return;
    Node *n;
    while (list) {
        n = list;
        list = list->next;
        freeNode(n);
    }
    return;
}

HashTable *initHashTable(int size) {
    HashTable *h = (HashTable *)malloc(sizeof(HashTable));
    h->size = 2 * size;
    h->data = (Node **)calloc(h->size, sizeof(Node*));
}

void freeHashTable(HashTable *h) {
    if (!h) return;
    for (int i = 0; i < h->size; i++) {
        freeList(h->data[i]);
    }
    free(h->data);
    free(h);
    return;
}

Node *insertNode(Node *head, Node *p) {
    p->next = head;
    return p;
}

int BKDHash(const char *str) {
    int seed = 11; // prime
    int hash = 0;
    while (*str) {
        hash = hash * seed + str[0];
        ++str;
    }
    return hash & 0x7fffffff;
}

int insertHash(HashTable *h, const char *str) {
    if (h == NULL) return 0;
    int hash = BKDHash(str);
    int idx = hash % h->size;

    h->data[idx] = insertNode(h->data[idx], initNode(str));

    return 1;
}

Node *searchList(Node *p, const char *str) {
    while (p && strcmp(p->str, str)) {
        p = p->next;
    }
    return p;
}

Node *search(HashTable *h, const char *str) {
    if (h == NULL) return NULL;
    int hash = BKDHash(str);
    int idx = hash % h->size;

    return searchList(h->data[idx], str);
}

char *makeStr(char *str, int n) {
    int len = rand() % (n - 1) + 1;
    char tmp;
    for (int i = 0; i < len; i++) {
        switch (rand() % 3) {
            case 0:
                tmp = 'A' + rand() % 26;
                break;
            case 1:
                tmp = 'a' + rand() % 26;
                break;
            case 2:
                tmp = '0' + rand() % 10;
                break;
        }
        str[i] = tmp;
    }
    str[n] = '\0'; // or str[n] = 0;
    return str;
}

int main(void) {
    srand(time(NULL));

    #define N 10
    char str[10];
    int cnt = N;
    HashTable *h = initHashTable(N);

    while (cnt--) {
        insertHash(h, makeStr(str, 10));
        printf("%s ", str);
    }
    putchar(10); // or putchar('\n');

    while (~scanf("%s", str)) {
        if (!strcmp(str, "q")) break; // q 退出
        Node *node = search(h, str);
        if (node)
            printf("hash=%d addr=%p str=%s\n", BKDHash(str), node, node->str);
        else
            printf("%s not found\n", str);
    }

    #undef N
    return 0;
}

查找表

用于查找的数据集合则称为 查找表（search table） 。查找表中的数据元素类型是一致的，并且有能够唯一标识出元素的 关键字（keyword） 。

通常对查找表有 4 种操作：

  1. 查找：在查找表中查看某个特定的记录是否存在
  2. 检索：查找某个特定记录的各种属性
  3. 插入：将某个不存在的数据元素插入到查找表中
  4. 删除：从查找表中删除某个特定元素

如果对查找表只执行前两种操作，则称这类查找表为 静态查找表（static search table） 。静态查找表建立以后，就不能再执行插入或删除操作，查找表也不再发生变化。比如顺序查找、折半查找、分块查找等。

对应的，如果对查找表还要执行后两种操作，则称这类查找表为 动态查找表（dynamic search table） 。对于动态查找表，往往使用二叉平衡树、B-树或哈希表来处理。

性能度量

使用 平均查找长度（average search length, ASL） 来衡量查找算法的性能。

假设每个元素时等概率分布，ASL就是所有元素被成功查找时，元素比较次数的期望。

通常平均查找长度，不考虑查找不成功的情况。

顺序查找

顺序查找（又称线性查找，sequential search） 是指在线性表中进行的查找算法。对于无序序列，查找成功的ASL为 \(\frac{n+1}{2}\)。查找不成功ASL为 n。

对于有序序列，查找成功的ASL为 \(\frac{n+1}{2}\)。查找不成功ASL为 \(\frac{n}{2} +\frac{n}{n+1}\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>

int search(int *data, int length, int value) {
    for (int i = 0; i < length; ++i) {
        if (data[i] == value) {
            return i;
        } else if (data[i] > value) {
            return -1;
        }
    }
    return -1;
}

int main() {
    int a[5] = {2, 4, 6, 8, 10};
    printf("%d\n", search(a, 5, 4));
    printf("%d\n", search(a, 5, 5));
    return 0;
}

折半查找

针对有序可随机寻址的顺序表结构，查找时间复杂度稳定下降为 \(O(log(n))\) 级别。

在定义端点下标时，决定了搜索区间的分布情况。右端定义为length - 1，搜索区间为闭区间。右端收缩为 mid - 1。右端定义为length，搜索区间为左闭右开，右端收缩为 mid。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>

int search(int *data, int length, int value) {
    int left = 0, right = length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (data[mid] == value) {
            return mid;
        } else if (data[mid] < value) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

int main() {
    int a[5] = {2, 4, 6, 8, 10};
    printf("%d\n", search(a, 5, 10));
    printf("%d\n", search(a, 5, 5));
    return 0;
}

搜索排好序的序列中某重复元素第一个出现位置的问题。

1
2
3
4
5
6
7
8
9
10
11
12
int search(int *data, int length, int value) {
    int left = 0, right = length;  // 处理不存在目标情况
    while (left < right) {
        int mid = (left + right) / 2;
        if (data[mid] == value) {
            right = mid; // 收缩到第一个出现位置
        } else {
            left = mid + 1;
        }
    }
    return right != length ? left : -1; // 处理不存在目标情况
}

搜索排好序的序列中某重复元素最后一个出现位置的问题。

1
2
3
4
5
6
7
8
9
10
11
12
int search(int *data, int length, int value) {
    int left = -1, right = length - 1;  // left = -1 处理不存在目标情况
    while (left < right) {
        int mid = (left + right + 1) / 2;  // 保证left不会恒定为一个值，所以 + 1
        if (data[mid] == value) {
            left = mid; // 收缩到第一个出现位置
        } else {
            right = mid - 1;
        }
    }
    return left;  // 不存在返回 -1
}

三分查找

适合序列具有凸性的情况，某一点两侧分别是单调的。

  1. 首先将区间 \([L, R]\) 平均分成三部分：\([L, m_1]\)、\([m_1, m_2]\)、\([m_2, R]\)。
  2. 计算三等分点 \(m_1\) 和 \(m_2\) 对应的函数值 \(f(m_1)\) 和 \(f(m_2)\)。
  3. 比较 \(f(m_1)\) 和 \(f(m_2)\) 的大小。 如果 \(f(m_1) > f(m_2)\)，则说明点 \(T\) 一定不在区间 \([m_2, R]\) 内，可以把右边界 \(R\) 更新成 \(m_2\)； 如果 \(f(m_1) < f(m_2)\)，则说明点 \(T\) 一定不在区间 \([L, m_1]\) 内，可以把左边界 \(L\) 更新成 \(m_1\)； 如果 \(f(m_1) = f(m_2)\)，则说明点 \(T\) 一定落在区间 \([m_1, m_2]\) 内。另外，可以将这种情况归为上面两种情况的任一一种。
  4. 重复以上操作，不断缩小查找区间，直到在精度要求的范围内，左边界 \(L\) 等于右边界 \(R\)，这时的边界点 \((L, f(L))\) 或者 \((R, f(R))\) 即是查找的极大值点 \(T\)。

同理，如果求凹性函数的极小值点，只需要在第三步中，将大于号和小于号反向变化一下即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <stdio.h>

int find_max(int *data, int length) {
    int left = 0, right = length - 1;
    while (right - left >= 2) {
        int m1 = left + (right - left) / 3;
        int m2 = right - (right - left + 2) / 3;
        if (data[m1] >= data[m2]) {
            right = m2;
        } else {
            left = m1 + 1;
        }
    }
    if (data[left] > data[right]) {
        return left;
    } else {
        return right;
    }
}

int main() {
    int a[5] = {1, 2, 7, 5, 4};
    printf("%d\n", find_max(a, 5));
    return 0;
}

分块查找

分块查找（Blocking Search）的基本思想是将一个线性表分成若干个子表，在查找时，先确定目标元素所在的子表再在该子表中去查找它。

分块查找也被叫做 索引顺序查找 ，在分块查找方法中，需要建立一个 索引表 。索引表中包含两类信息：关键字和指针。关键字指的每个子表中最大的关键字，指针则表示该子表中第一个元素在整个表中的下标。

分块查找要求整个线性表是分块有序的。第 i 个子表中最大的关键字小于第 i+1 个子表中最小的关键字。

而在每一个子表中，元素的排列是随意的，只能通过顺序查找的方法在子表中完成最终的查找工作。

分块查找的效率是基于顺序查找和折半查找之间的。先搜索引，再顺序搜索子表。

分块查找的优势在于，由于子块中的元素是随意排序的，只要找到对应的块就能直接进行插入和删除操作，而不用大量移动其它的元素，因此它适用于线性表需要频繁的动态变化的情况。

分块查找的缺点则在于它需要一定的内存空间来存放索引表并且要求对索引表进行排序。

C++ STL中的deque就是使用这种分块的“连续”结构设计思路。

排序

根据算法的时间复杂度，可以将排序算法分为复杂度为 \(O(n^2),\ O(n\log(n)),\ O(n)\)等时间复杂度的排序算法。比如 \(O(n)\) 的 基数排序（radix sort）、 \(O(n\log(n))\)的归并排序、\(O(n^2)\)的冒泡排序。

根据排序过程中元素是否完全保存在内存中，可以将算法分为 内部排序（internal sort） 和 外部排序（external sort） 。

对于一个排序算法，如果任意两个元素 \(a_i\) 和 \(a_j\) 在排序前的线性表中满足条件 i<j 且 \(a_i = a_j\)，在排序后 \(a_i\) 仍在 \(a_j\) 之前，则称这个排序算法为 稳定排序（stable sort） (比如插入、冒泡、归并)，否则称这个排序算法为 不稳定排序(unstable sort) （选择、快速、堆、希尔排序）。

插入排序

将线性表分为已排序的前半部分和待排序的后半部分，从待排序部分选出第一个元素，插入到已排序部分的对应位置中，直到全部记录都插入到已排序部分中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void print(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", data[i]);
    }
    printf("\n");
}

void sort(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        for (int j = i - 1; j >= 0; --j) {
            if (data[j] > data[j + 1]) {
                swap(&data[j], &data[j + 1]);
            } else {
                break;
            }
        }
    }
}

void sort_better(int *data, int length) {
    int cur;
    for (int i = 1; i < length; i++) {
        cur = data[i];
        int j = i - 1;
        while (j >= 0 && data[j] > cur) {
            data[j + 1] = data[j];
            j--;
        }
        data[j + 1] = cur;
    }
}

int main() {
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    sort(arr, n);
    print(arr, n);
    return 0;
}

冒泡排序

从前往后两两比较相邻元素的关键字， 按照目标大小顺序进行交换元素，每趟交换以后最后一个元素一定是最大的，不再参与下一趟交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <stdio.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void print(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", data[i]);
    }
    printf("\n");
}

void sort(int *data, int length) {
    for (int i = 0; i < length - 1; ++i) {
        int swapped = 0;
        for (int j = 0; j < length - i - 1; ++j) {
            if (data[j] > data[j + 1]) {
                swap(&data[j], &data[j + 1]);
                swapped = 1;
            }
        }
        if (swapped == 0) {
            break;
        }
    }
}

void sort_better(int *data, int len) {
    int isSorted = 0;
    do {
        isSorted = 1;
        len--;
        for (int i=0; i<len; ++i) {
            if (data[i] > data[i+1]) {
                isSorted = 0;
                swap(&data[i], &data[i+1]);
            }
        }
    } while (!isSorted);
}

int main() {
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    sort(arr, n);
    print(arr, n);
    return 0;
}

归并排序

设法将两个有序的线性表组合成一个新的有序线性表。为了实现归并操作，每次合并都需要开辟额外的空间来临时保存合并后的排序结果，总共需要开辟 n 个元素的空间，所以归并排序的空间复杂度为 \(O(n)\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void print(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", data[i]);
    }
    printf("\n");
}

void mergesort(int *data, int l, int r) {
    if (l == r) return;
    int mid = (l + r) / 2;
    mergesort(data, l, mid);
    mergesort(data, mid + 1, r);

    int temp[r - l + 1]; // 或者从堆分配空间
    int x = l, y = mid + 1, loc = 0;
    while (x <= mid || y <= r) {
        if (x <= mid && (y > r || data[x] <= data[y])) 
            temp[loc] = data[x++];
        else
            temp[loc] = data[y++];
        loc++;
    }

    for (int i = l; i <= r; i++) {
        data[i] = temp[i - l];
    }
}

int main() {
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    merge_sort(arr, 0, n - 1);
    print(arr, n);
    return 0;
}

选择排序

选择排序，每趟从线性表的待排序区域选取关键字最小的元素，将其放到已排序区域的最后。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <stdio.h>

inline void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void print(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", data[i]);
    }
    printf("\n");
}

void sort(int *data, int length) {
    int temp;
    for (int i = 0; i < length - 1; ++i) {
        temp = i;
        for (int j = i + 1; j < length; ++j) {
            if (data[temp] > data[j]) {
                temp = j;
            }
        }
        if (i != temp) {
            swap(&data[i], &data[temp]);
        }
    }
}

void sort_better(int *data, int len) {
    if (len <= 1) return;
    register int *last = data + len - 1,
    			 *p,
    			 *minPtr;
    for ( ; data < last; ++data) {
        minPtr = data;
        for (p = data + 1; p <= last; ++p) {
            if (*p < *minPtr) minPtr = p;
        }
        swap(minPtr, data);
    }
}

int main() {
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    sort(arr, n);
    print(arr, n);
    return 0;
}

在每次查找关键字最小的元素时，可以使用堆对效率进行优化，使用堆来优化的选择排序就是堆排序。

快速排序

快速排序是目前应用最广泛的排序算法之一。它的基本思想是，每次从待排序区间选取一个元素（在后面的课程中都是选取第一个）作为基准记录，所有比基准记录小的元素都在基准记录的左边，而所有比基准记录大的元素都在基准记录的右边。之后分别对基准记录的左边和右边两个区间进行快速排序，直至将整个线性表排序完成。

quick_sort_better 实现了单边递归，将两个递归函数，优化成一个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void print(int *data, int length) {
    for (int i = 0; i < length; ++i) {
        if (i > 0) {
            printf(" ");
        }
        printf("%d", data[i]);
    }
    printf("\n");
}

void quick_sort(int *data, int left, int right) {
    if (left > right) {
        return;
    }
    int pivot = data[left], low = left, high = right;
    while (low < high) {
        while (low < high && data[high] >= pivot) {
            high--;
        }
        data[low] = data[high];
        while (low < high && data[low] <= pivot) {
            low++;
        }
        data[high] = data[low]; 
    }
    data[low] = pivot;
    
    quick_sort(data, left, low - 1);
    quick_sort(data, low + 1, right);
}

// quick sort 优化
void quick_sort_better(int *data, int l, in r) {
    if (l >= r) return;
    while (l < r) {
        int x = l, y = r, pivot = data[(x + (y - x)) / 2];
        while (x <= y) {
           	while (data[x] < pivot) ++x;
            while (data[y] > pivot) --y;
            if (x <= y) {
                swap(&data[x++], &data[y--]);
            }
        }
    	quick_sort_better(data, l, y);
        l = x; // 直接在当前函数内，快排后半部分
    }
    return;
}

int main() {
    int n;
    scanf("%d", &n);
    int arr[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    quick_sort(arr, 0, n - 1);
    print(arr, n);
    return 0;
}

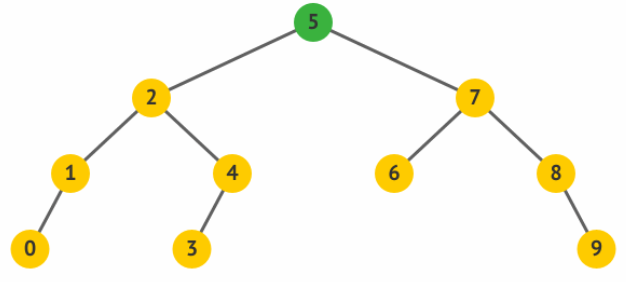
二叉查找树

对任意结点，如果左子树不为空，则左子树上所有结点的权值都小于该结点的权值；如果右子树不为空，则右子树上所有结点的权值都大于该结点的权值。

如果中序遍历二叉查找树，会得到一个从小到大的序列。

在二叉查找树的基础上可以加些优化，可以让其成为 AVL 树，红黑树，SBT，Splay 等等，这些高级的树结构解决了二叉树退化的问题。

插入过程：

  1. 根节点为空则新元素直接作为根节点，否则传入的参数 value 与根节点进行比较。
  2. value 等于当前节点则直接返回，小于则跳转到步骤 3，而如果 value 大于当前节点时，跳转到步骤 4。
  3. 判断当前节点是否存在左孩子，如果存在则让其左孩子继续调用插入方法，回到步骤 2，如果不存在则将新元素插入到当前节点的左孩子位置上。
  4. 判断当前节点是否存在右孩子，存在则让其右子树继续调用插入方法，回到步骤 2，不存在则将新元素插入到当前节点的右孩子位置上。

简单实现插入和查找，输出中序遍历结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node *lchild, *rchild, *father;
}Node;

Node* init(int data, Node *father) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->data = data;
    node->lchild = NULL;
    node->rchild = NULL;
    node->father = father;
    return node;
}

Node* insert(int value, Node *tree) {
    if (!tree) {
        tree = init(value, NULL);
        return tree;
    }
    if (value > tree->data) {
        if (!tree->rchild)
            tree->rchild = init(value, tree);
        else
            tree->rchild = insert(value, tree->rchild);
    } else {
        if (!tree->lchild)
            tree->lchild = init(value, tree);
        else
            tree->lchild = insert(value, tree->lchild);
    }
    return tree;
}

Node* search(int value, Node *tree) {
    if (!tree || value == tree->data)
        return tree; 
    if (value > tree->data) {
        if (!tree->rchild)
            return NULL;
        else
            return search(value, tree->rchild);
    } else {
        if (!tree->lchild)
            return NULL;
        else
            return search(value, tree->lchild);
    }
}

void inorder(Node *tree) {
    if (!tree) return;
    inorder(tree->lchild);
    printf("%d ", tree->data);
    inorder(tree->rchild);
}

void clear(Node *node) {
    if (node != NULL) {
        if (node->lchild != NULL) {
            clear(node->lchild);
        }
        if (node->rchild != NULL) {
            clear(node->rchild);
        }
        free(node);
    }
}

int main() {
    Node *binarytree = NULL;
    init(100, binarytree);
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        int v;
        scanf("%d", &v);
        binarytree = insert(v, binarytree);
    }
    int value;
    scanf("%d", &value);
    if (search(value, binarytree)) {
        printf("search success!\n");
    } else {
        printf("search failed!\n");
    }

    (void)inorder(binarytree);

    clear(binarytree);
    return 0;
}

删除操作

节点的前驱指的是值比它小的节点中最大的一个节点，后继是指值比它大的节点中最小的一个。

查找节点前驱的算法流程如下：

  1. 找到当前节点的左孩子，如果当前节点没有左孩子则不存在前驱，若存在，则找到其左孩子的右孩子。
  2. 若当前节点有右孩子则继续找到其右孩子，重复步骤 2，直至找到一个节点不存在右孩子时，那么它就是要查找的前驱。

删除操作的算法流程如下：

  1. 找到被删除的节点。
  2. 若它存在左孩子，则找到他的前驱，用前驱替换被删除节点的值，再调用删除节点的方法删除前驱。
  3. 若被删除节点不存在左孩子，则找到它的后继，用后继替换被删除节点的值，再调用删除节点的方法删除后继。
  4. 若被删除的节点不存在孩子节点，直接调用删除节点的的方法删除它。

实现删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct Node {
    int data;
    struct Node *lchild, *rchild, *father;
}Node;

Node* init(int _data, Node *_father) {
    Node *node =(Node *)malloc(sizeof(Node));
    node->data = _data;
    node->lchild = NULL;
    node->rchild = NULL;
    node->father = _father;
    return node;
}

Node* insert(Node *node, int value) {
    if (node == NULL) {
        node = init(value, NULL);
    } else if (value > node->data) {
        if (node->rchild == NULL) {
            node->rchild = init(value, node);
        } else {
            node->rchild = insert(node->rchild, value);
        }
    } else if (value < node->data) {
        if (node->lchild == NULL) {
            node->lchild = init(value, node);
        } else {
            node->lchild = insert(node->lchild, value);
        }
    }
    return node;
}

Node* search(Node *node, int value) {
    if (node == NULL || node->data == value) {
        return node;
    } else if (value > node->data) {
        if (node->rchild == NULL) {
            return NULL;
        } else {
            return search(node->rchild, value);
        }
    } else {
        if (node->lchild == NULL) {
            return NULL;
        } else {
            return search(node->lchild, value);
        }
    }
}

Node* predecessor(Node *node) {
    if (!node->lchild) return NULL;
    Node *res = node->lchild;
    while (res && res->rchild) {
        res = res->rchild;
    }
    return res;
}

Node* successor(Node *node) {
    if (!node->rchild) return NULL;
    Node *res = node->rchild;
    while (res && res->lchild) {
        res = res->lchild;
    }
    return res;
}

// 删除度为1或者0的节点，在delete_tree函数中使用。
void remove_node(Node *node) {
    if (!node) return;
    Node *tmp = NULL;
    if (node->lchild) {
        tmp = node->lchild;
        tmp->father = node->father;
    }
    if (node->rchild) {
        tmp = node->rchild;
        tmp->father = node->father;
    }

    if (node->father->lchild == node) {
        node->father->lchild = tmp;
    } else {
        node->father->rchild = tmp;
    }
    node->rchild = NULL;
    node->lchild = NULL;
    node->father = NULL;
    free(node);
}

// 根据输入值删除节点
int delete_tree(Node *tree, int value) {
    if (!tree) return ERROR;
    Node *target = search(tree, value);
    if (!target) return ERROR;

    Node *tmp = NULL;
    if (target->lchild) {
        tmp = predecessor(target);
    } else if (target->rchild) {
        tmp = successor(target);
    } else {
        tmp = target;
    }
    target->data = tmp->data;
    remove_node(tmp);
    return OK;
}

void clear(Node *node) {
    if (node != NULL) {
        if (node->lchild != NULL) {
            clear(node->lchild);
        }
        if (node->rchild != NULL) {
            clear(node->rchild);
        }
        free(node);
    }
}

int main() {
    Node *binarytree = NULL;
    int arr[10] = { 8, 9, 10, 3, 2, 1, 6, 4, 7, 5 };
    for (int i = 0; i < 10; i++) {
        binarytree = insert(binarytree, arr[i]);
    }
    int value;
    scanf("%d", &value);
    if (search(binarytree, value) != NULL) {
        printf("search success!\n");
    } else {
        printf("search failed!\n");
    }
    
    scanf("%d", &value);
    if (delete_tree(binarytree, value)) {
        printf("delete success!\n");
    } else {
        printf("delete failed!\n");
    }
    
    clear(binarytree);
    return 0;
}

平衡二叉树

所有平衡二叉查找树基本由以下三个特征组成：

  1. 自平衡条件

  2. 旋转操作

  3. 旋转的触发

平衡二叉查找树通过设置合理的自平衡条件，使得二叉查找树的查找、插入等操作的性能不至于退化成 \(O(n)\).

AVL 树是最早发明的一种平衡二叉查找树。

AVL

AVL 树提出了一个概念： 平衡因子（balance factor） 。每个结点的平衡因子是指它左子树最大高度和右子树最大高度的差。

在 AVL 树中，平衡因子为 −1、 0、 1 的结点都被认为是平衡的，而平衡因子为 −2、 2 等其他值的结点被认为是不平衡的，需要对这个结点所在子树进行调整。

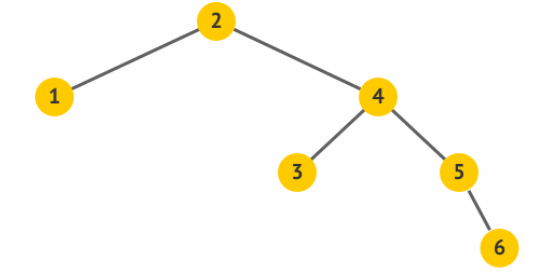
旋转

在 AVL 树中，一共有两种单旋操作：左旋和右旋。AVL 树通过一系列左旋和右旋操作，将不平衡的树调整为平衡二叉查找树。

旋转前

左旋转

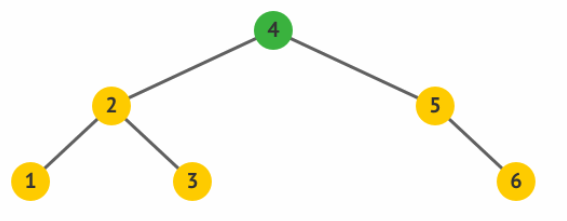
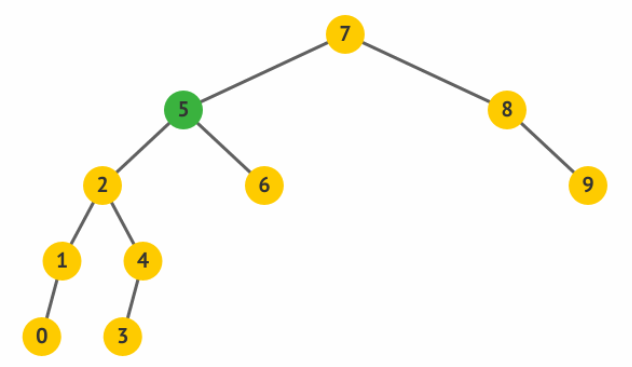
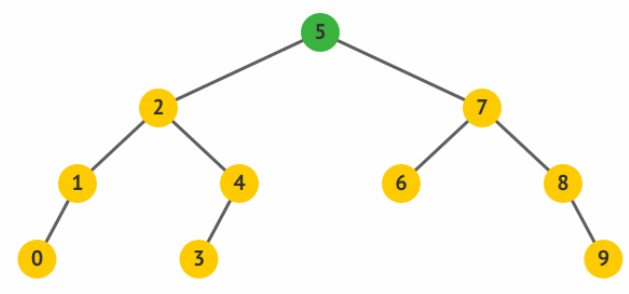
通过进行左旋操作，使得原先的根 2 变成了其右孩子 4 的左孩子，而 4 原先的左孩子 3 变成了 2 的右孩子。

旋转前

右旋转

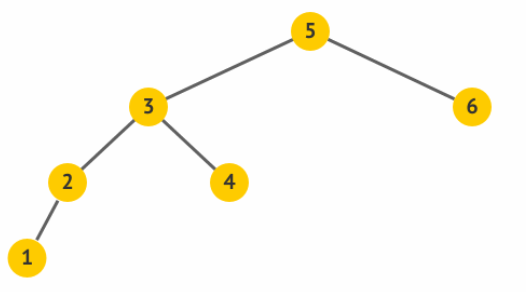
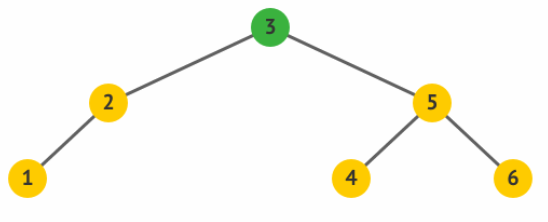
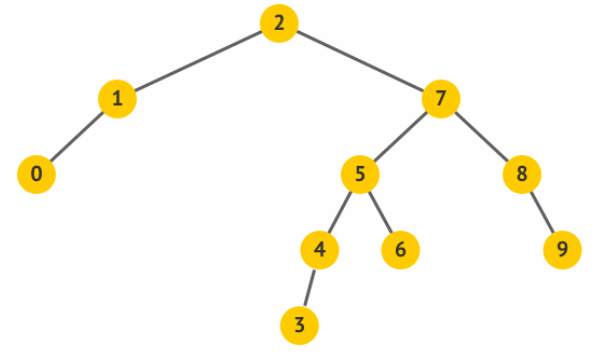
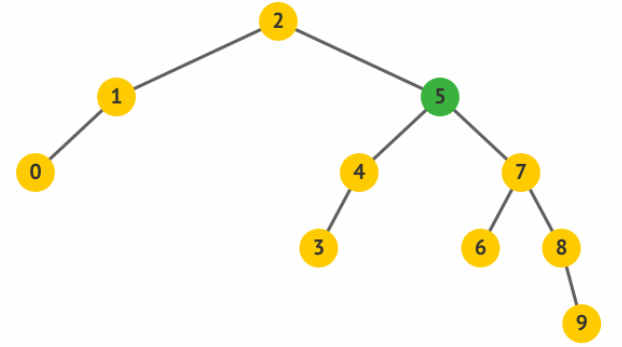
通过右旋操作，使得原先的根 5 变成了其左孩子 3 的右孩子，而 3 原先的右孩子变成了 5 的左孩子。

AVL 树中还有两种复合旋转操作（即“多旋”），由两次单旋操作组合而成。

左旋加右旋：

image-20211005112345360

右旋加左旋：

旋转的触发

在插入一个元素后不断回溯的过程中，如果因此导致结点不平衡，则根据不平衡情况（一定是一边子树比另一边子树的高度大 2）进行对应的旋转：

  1. 左子树比右子树的高度大 2：

  • 如果新增元素插入到左儿子的左子树中，则进行右旋操作。( LL 型调整 )

  • 如果新增元素插入到左儿子的右子树中，则进行左旋加右旋操作。（ LR 型调整 ）

    1. 右子树比左子树的高度大 2：

  • 如果新增元素插入到右儿子的右子树中，则进行左旋操作。（ RR 型调整 ）

  • 如果新增元素插入到右儿子的左子树中，则进行右旋加左旋操作。（ RL 型调整 ）

类似的，在删除一个元素后不断回溯的过程中，如果出现结点不平衡，则和插入操作采用相同的调整操作，确保在删除以后整棵树依然是平衡的。

Size Balanced Tree

对于 SBT，它的自平衡条件会显得稍微复杂一些：对于每个结点 t，同时满足： $$ size[right[t]]≥max(size[left[left[t]]],size[right[left[t]]]) \

size[left[t]]≥max(size[left[right[t]]],size[right[right[t]]]) $$ size表示以该节点为根的子树中节点个数。

每个结点所在子树的结点个数，不小于其兄弟的两个孩子所在子树的结点个数的最大值。

旋转操作和 AVL 树的左旋右旋是完全一样的。

只是旋转的触发条件不同。

旋转的触发

在调整过程中，一共有 4 种会触发旋转的情况：

  1. LL 型（ size[left[left[t]]] > size[right[t]] ）：首先对子树 t 执行右旋操作，旋转以后对 t 的右子树进行调整，之后再对子树 t 进行调整。
  2. LR 型（ size[right[left[t]]] > size[right[t]] ）：首先对 t 的左子树执行左旋操作，再对 t 进行右旋操作。之后分别调整结点 t 的左右子树，最终对结点 t进行调整。
  3. RR 型（ size[right[right[t]]] > size[left[t]] ）：首先对 t 执行左旋操作，旋转以后对 t 的左子树进行调整，之后再对 t 进行调整。
  4. RL 型（ size[left[right[t]]] > size[left[t]] ）：首先对结点 t 的右子树执行右旋操作，再对 t 进行左旋操作。之后分别调整 t 的左右子树，最终对 t 进行调整。

通过递归的进行调整，让不平衡的 SBTree 恢复平衡状态。

简化流程：

  1. 如果在处理左子树更高的情况：
    1. LL 型：右旋 t。
    2. LR 型：左旋 t 的左子树，再右旋 t。
  2. 如果在处理右子树更高的情况：
    1. RR 型：左旋 t。
    2. RL 型：右旋 t 的右子树，再左旋 t。
  3. 递归调整左子树中左子树的左子树更高的情况。
  4. 递归调整右子树中右子树的右子树更高的情况。
  5. 递归调整当前子树中左子树更高的情况。
  6. 递归调整当前子树中右子树更高的情况。

和 AVL 不太一样的是，SBTree 只有在插入时才可能触发调整，而不需要在删除结点以后进行调整 。

从理论上说，SBTree 和 AVL 树相比在均摊时间复杂度上没有区别，每次查询、插入和删除的时间复杂度都为 \(O(\log(n))\)。

在实际运用中，SBTree 在查询操作较多的情况下会有效率上的优势。加之为了维护平衡性记录了每个结点所在子树大小（即子树内结点个数），相比其他平衡二叉查找树而言，更便于求解第 k 大元素、或求解元素的秩（rank）等类似问题。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
#include <stdio.h>
#include <stdlib.h>

#define ERROR 0
#define OK 1

typedef struct SBTNode {
    int data, size;
    struct SBTNode *lchild, *rchild, *father;
}SBTNode;

SBTNode* init(int init_data, int init_size, SBTNode *init_father);

SBTNode *NIL;

void init_NIL() {
    NIL = (SBTNode *)malloc(sizeof(SBTNode));
    NIL->data = 0;
    NIL->size = 0;
    NIL->lchild = NIL;
    NIL->rchild = NIL;
    NIL->father = NULL;
}

SBTNode* init(int init_data, int init_size, SBTNode *init_father) {
    SBTNode *node = (SBTNode *)malloc(sizeof(SBTNode));
    node->data = init_data;
    node->size = init_size;
    node->lchild = NIL;
    node->rchild = NIL;
    node->father = init_father;
    return node;
}

// 左旋实现，复杂一点的链表指向关系转移
SBTNode* left_rotate(SBTNode *node) {
    SBTNode *temp = node->rchild;
    node->rchild = temp->lchild;
    temp->lchild->father = node;
    temp->lchild = node;
    temp->father = node->father;
    node->father = temp;
    temp->size = node->size;
    node->size = node->lchild->size + node->rchild->size + 1;
    return temp;
}

// 右旋实现，旋转操作的根节点为node
SBTNode* right_rotate(SBTNode *node) {
    SBTNode *temp = node->lchild;
    node->lchild = temp->rchild;
    temp->rchild->father = node;
    temp->rchild = node;
    temp->father = node->father;
    node->father = temp;
    temp->size = node->size;
    node->size = node->lchild->size + node->rchild->size + 1;
    return temp;
}

// 递归调整平衡二叉树，以size为对比标准，flag指示子树哪一边size更大
SBTNode* maintain(SBTNode *node, int flag) {
    if (flag == 0) {
        // 左子树中左子树size 大于 node的右子树，LL情况，使用右旋调整
        if (node->lchild->lchild->size > node->rchild->size) {
            node = right_rotate(node);
        } 
        // LR, 先左旋再右旋
        else if (node->lchild->rchild->size > node->rchild->size) {
            node->lchild = left_rotate(node->lchild);
            node = right_rotate(node);
        } else {
            return node;
        }
    } else {
        // RR, 左旋
        if (node->rchild->rchild->size > node->lchild->size) {
            node = left_rotate(node);
        } 
        // RL，先右旋再左旋
        else if (node->rchild->lchild->size > node->lchild->size) {
            node->rchild = right_rotate(node->rchild);
            node = left_rotate(node);
        } else {
            return node;
        }
    }
    
    // 递归处理左右子树
    node->lchild = maintain(node->lchild, 0);
    node->rchild = maintain(node->rchild, 1);
    // 当子树调整后，再处理 node 的平衡
    node = maintain(node, 0);
    node = maintain(node, 1);
    return node;
}

SBTNode* insert(SBTNode *node, int value) {
    node->size++;
    if (value > node->data) {
        if (node->rchild == NIL) {
            node->rchild = init(value, 1, node);
        } else {
            node->rchild = insert(node->rchild, value);
        }
    } else {
        if (node->lchild == NIL) {
            node->lchild = init(value, 1, node);
        } else {
            node->lchild = insert(node->lchild, value);
        }
    }
    return maintain(node, value > node->data);
}

SBTNode* search(SBTNode *node, int value) {
    if (node == NIL || node->data == value) {
        return node;
    } else if (value > node->data) {
        if (node->rchild == NIL) {
            return NIL;
        } else {
            return search(node->rchild, value);
        }
    } else {
        if (node->lchild == NIL) {
            return NIL;
        } else {
            return search(node->lchild, value);
        }
    }
}

SBTNode* insert_node(SBTNode *node, int value) {
    if (node == NULL) {
        node = init(value, 1, NULL);
        return node;
    }
    if (search(node, value) != NIL) {
        return node;
    }
    return insert(node, value);
}


SBTNode* predecessor(SBTNode *node) {
    SBTNode *temp = node->lchild;
    while (temp != NIL && temp->rchild != NIL) {
        temp = temp->rchild;
    }
    return temp;
}

SBTNode* successor(SBTNode *node) {
    SBTNode *temp = node->rchild;
    while (temp != NIL && temp->lchild != NIL) {
        temp = temp->lchild;
    }
    return temp;
}

void remove_node(SBTNode *delete_node) {
    SBTNode *temp = NIL;
    if (delete_node->lchild != NIL) {
        temp = delete_node->lchild;
        temp->father = delete_node->father;
        delete_node->lchild = NIL;
    }
    if (delete_node->rchild != NIL) {
        temp = delete_node->rchild;
        temp->father = delete_node->father;
        delete_node->rchild = NIL;
    }
    if (delete_node->father->lchild == delete_node) {
        delete_node->father->lchild = temp;
    } else {
        delete_node->father->rchild = temp;
    }
    temp = delete_node;
    while (temp != NULL) {
        temp->size--;
        temp = temp->father;
    }
    delete_node->lchild = NIL;
    delete_node->rchild = NIL;
    free(delete_node);
}

int delete_tree(SBTNode *node, int value) {
    SBTNode *delete_node, *current_node;
    current_node = search(node, value);
    if (current_node == NIL) {
        return ERROR;
    }
    if (current_node->lchild != NIL) {
        delete_node = predecessor(current_node);
    } else if (current_node->rchild != NIL) {
        delete_node = successor(current_node);
    } else {
        delete_node = current_node;
    }
    current_node->data = delete_node->data;
    remove_node(delete_node);
    return OK;
}

void inorder(SBTNode *node) {
    if (node == NIL) return;
    inorder(node->lchild);
    printf("%d ", node->data);
    inorder(node->rchild);
    return;
}

void clear(SBTNode *node) {
    if (node != NIL) {
        if (node->lchild != NIL) {
            clear(node->lchild);
        }
        if (node->rchild != NIL) {
            clear(node->rchild);
        }
        free(node);
    }
}

int main() {
    init_NIL();
    SBTNode *binarytree = NULL;
    int arr[10] = { 8, 9, 10, 3, 2, 1, 6, 4, 7, 5 };
    for (int i = 0; i < 10; i++) {
        binarytree = insert_node(binarytree, arr[i]);
    }
    int value;
    scanf("%d", &value);
    if (search(binarytree, value) != NIL) {
        printf("search success!\n");
    } else {
        printf("search failed!\n");
    }    
    scanf("%d", &value);
    if (delete_tree(binarytree, value)) {
        printf("delete success!\n");
    } else {
        printf("delete failed!\n");
    }
    clear(binarytree);
    return 0;
}

求解第k小元素

只需要在SBTree基础上，增加一个函数 select_a。SBTree记录了树的size，所以找到某个大小的元素比较便利。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
...
int select_a(SBTNode *node, int k) {
    int rank = node->lchild->size + 1;
    if (rank == k) {
        return node->data;
    } else if (k < rank) {
        return select_a(node->lchild, k);
    } else {
        return select_a(node->rchild, k - rank);
    }
}

int main() {
    init_NIL();
    SBTNode *binarytree = NULL;
    int arr[10] = { 8, 9, 10, 3, 2, 1, 6, 4, 7, 5 };
    for (int i = 0; i < 10; i++) {
        binarytree = insert_node(binarytree, arr[i]);
    }
    int k;
    scanf("%d", &k);
    printf("%d\n", select_a(binarytree, k));
    clear(binarytree);
    return 0;
}

RBTree

红黑树（Red-Black Tree） 也是一种自平衡的二叉查找树。1972 年由 Rudolf Bayer 发明的，而“红黑树”的名字是由 Leo J. Guibas 和 Robert Sedgewick （写 《算法》的普林斯顿大佬）于 1978 年首次提出。

红黑树相比于 AVL，牺牲了部分平衡性以在插入、删除操作时减少旋转操作，整体性能优于 AVL，也正因如此，C++ STL 中的 map 就是用红黑树实现的。

红黑树和其他平衡二叉查找树相比，增加了一个 颜色 属性，用来标识树上的结点是红色还是黑色；并且如果一个结点没有子结点，则该结点的子节点对应的指针为 NIL，也就是说，红黑树的所有叶子都是 NIL。

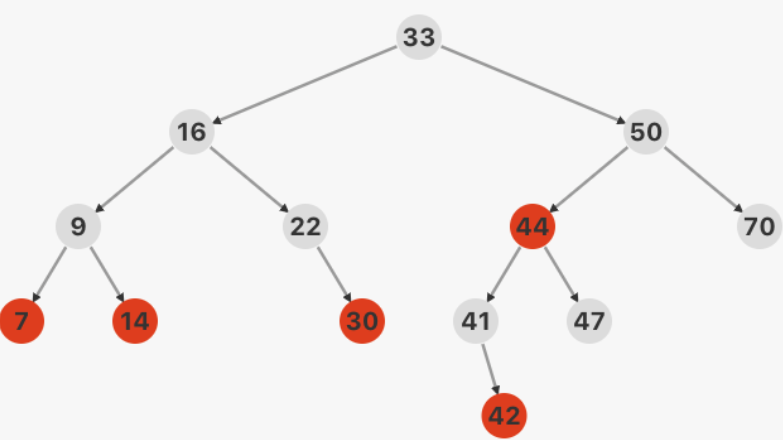
红黑树是满足如下条件的二叉查找树：

  1. 每个结点要么是红色，要么是黑色；
  2. 根结点是黑色；
  3. 叶结点（NIL）是黑色；
  4. 如果一个结点是红色，则它的两个子节点都是黑色的；
  5. 从根结点出发到所有叶结点的路径上，均包含相同数目的黑色结点。

第五条规则是红黑树平衡性的核心。

因为第四条和第五条规则的限制，使得红黑树上从根结点到每个叶结点的最长路径最多是最短路径的两倍，这也确保了整棵二叉查找树是平衡的。

一个省略NIL的合法红黑树

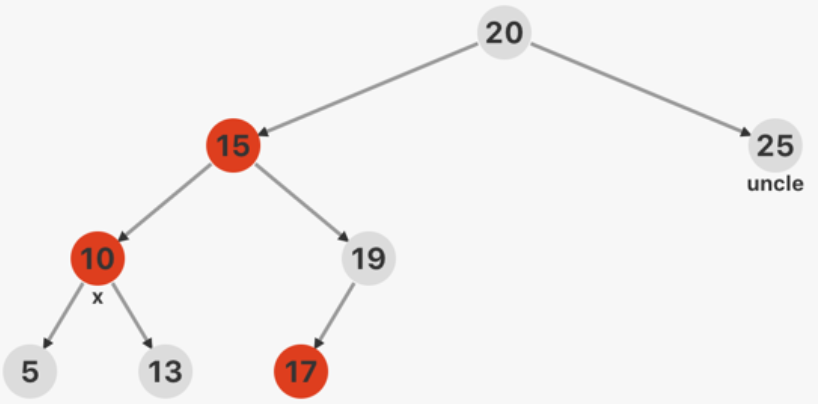
红黑树插入

插入分为四种情况，且插入节点默认为红色：

  1. 新结点 x 位于树的根

    根据第二条规则，将新结点的颜色改为黑色。

  2. x 的叔父结点（父节点的兄弟）是红色

    此时 x 的祖父结点一定是黑色的。

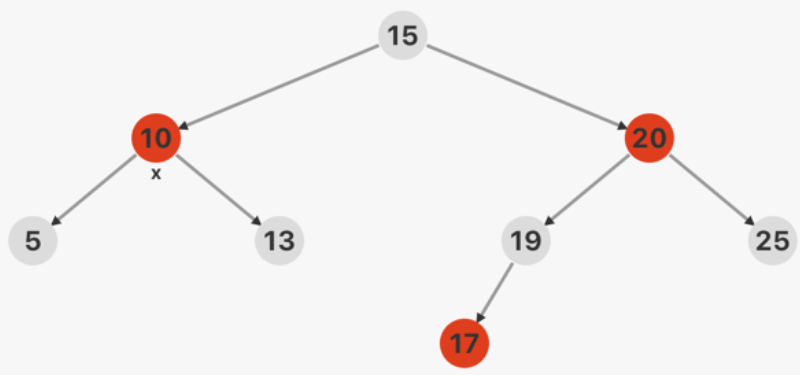
    将祖父结点的黑色改为红色，并将 x 的父结点和叔父结点改为黑色。之后将 x 的祖父结点作为 x 继续向上迭代（直到根节点）。

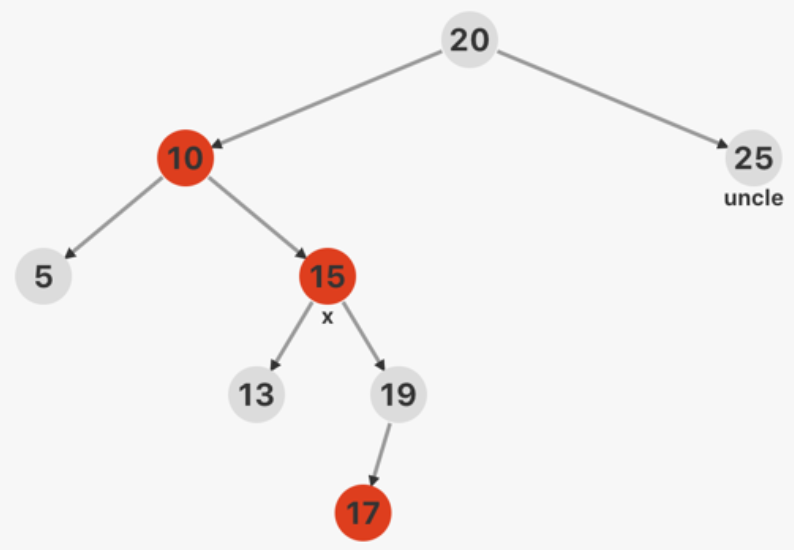
  3. x 的叔父结点是黑色的，并且 x 是一个右孩子

    对 x 的父结点进行左旋，原父结点仍为红色，叔父结点仍为黑色。进行第四种情况操作，且在第四种情况中，x代表左旋前的父节点。

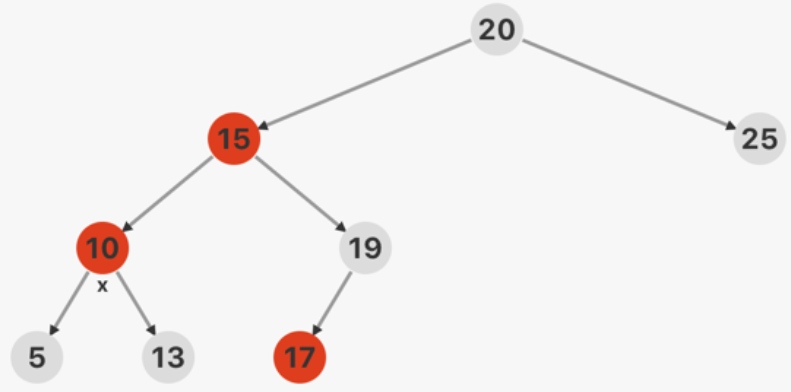
  4. x 的叔父结点是黑色的，并且 x 是一个左孩子

    将 x 的父结点改为黑色，祖父结点改为红色，并对 x 的祖父结点进行右旋。

删除操作不写了，有点麻烦，也没那个兴趣从头实现，比较复杂的算法，照着伪代码实现挺耗时间的。

多路平衡二叉树

在数据量较大的工程应用（如数据库）中，由于树中的结点信息往往保存在磁盘而非内存里，维护一棵平衡二叉查找树会导致大量的磁盘寻址和读写操作。而磁盘存取的时间要比 CPU 运算的时间更长。

为了解决这个问题，可以通过每次存取连续多个数据项，来减少磁盘读写的时间开销。

平衡树是检索效率非常高的一类数据结构，但平衡树每个结点只能保存一个关键字。为了便于一次从磁盘中读入连续的多个数据，多路查找树来了。

将二叉查找改为多路查找，可以在降低查找深度的同时，在同一个结点内维护更多的信息，每次存取连续多个数据项，降低磁盘寻址和读写的时间开销，优化在磁盘上检索数据的性能。

多路查找树（Multi-way search tree） 是指树中结点最多有 M 个孩子。查找的时间效率依然可以保证为 \(O(\log(n))\) 复杂度，并且树的深度更小。

2-3树

在 2-3 树中，有两种结点：2-node 和 3-node，表示每个结点有 2 个还是 3 个孩子。

树中的 所有叶子结点都在同一层 ，叶子结点可以包含一个或两个关键字。

2-node 一定 有两个孩子和一个关键字；3-node 一定 有三个孩子和两个关键字。

3-node有三个子树，两个关键字的值划分了三段连续的区间，三个子树分别位于这三个区间内。

B树

一棵最小度数为 t (t >= 2) 的 B 树除了满足多路查找树的基本性质以外，还满足如下的性质：

  • 根结点至少有一个关键字，以及两个孩子结点；
  • 所有内部结点至少有 t 个孩子结点，至多有 2t 个孩子结点；
  • 所有内部结点至少有 t−1 个关键字，至多有 2t−1 个关键字；
  • 每个叶子结点没有孩子。

查找

1
2
3
4
5
6
7
8
9
search(node, key)
    i = 0
    while i < node->count and key > node->keys[i]
        i = i + 1
    if i < node->count and key == node->keys[i]
        return (node, i)
    else if node->is_leaf
        return NIL
    else return search(node->childs[i], key)

每个node有count个子节点。

插入

节点的子节点个数是可以变化的，所以当达到一个节点的最大度数（或者关键字个数）需要将子节点中合适的关键字提升到父节点中，若父节点也满了，就继续提升。划分出更小的节点，再进行插入。

删除

B 树的删除操作需要在递归过程中确保所在结点的关键字个数 不小于 最小度数 t。

B+ 树

B+ 树和 B 树的不同之处在于：

  1. 所有关键字都存放在叶结点中，非叶结点的关键字表示的是子树中所有关键字的最小值，这被称为 最小复写码 。也可以统一存储子树所有关键字的最大值。
  2. 叶结点包含了全部的关键字信息，并且叶结点之间按从小到大的顺序链接。
  3. 非叶子结点内并不需要真正保存关键字的具体信息，因此整体的磁盘读写开销会更小。
  4. 遍历叶子结点就可以从小到大遍历相邻的元素。

因此，现有的数据库索引大多采用 B+ 树作为索引数据结构。

B * 树

在 B* 树中，内部结点（非根、非叶子）也增加了一个指向兄弟的指针。并且每个结点的关键字个数至少为关键字个数上限的 \(\frac{2}{3}\)。因为对下限的调整，所以 B * 树的空间使用率比 B 树和 B+ 树更高。