字符串匹配从KMP到AC自动机

Knuth-Morris-Pratt

在一个字符串S内查找一个词W的出现位置。KMP目的是什么？比如是暴力匹配（两个for循环）最坏的情况，O(m*n)：

1
2
S: aaaaaaaaaaaaaa
W: aaab

想法，不匹配就只是个结果，没有其它信息产生吗？显然，如果有一部分匹配，后续搜索应该可以利用。

怎么利用？

首先，有一部分匹配，才可以操作，才有多的信息嘛。

那么，目的就是保证已经匹配的部分，在S中，不再重复匹配。

1
2
S: aaaaaababaaaaa
W: ababc

比如，上例，abab匹配，c不匹配，重新回退4个位置匹配吗？W的信息我们是知道的，这末端abc不匹配，里面还有aba啊，并且从S当前匹配的信息，发现aba，已经再次匹配，S的指针不需要回退！

现在的问题，是W的信息怎么表示？需要什么信息？部分子串前缀和后缀相同的信息。

只需要一个数组，告诉我们，当出现不匹配字符时，可以跳过那些重复的一定会再次匹配的部分。

现在，问题就是：找到 W 对应的回退数组N，顺序匹配 S 与 W，按照 N 的信息回退。

时间复杂度：O(|S|+|W|)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
#include <string>

using namespace std;

void get_backoff(string &pattern, vector<int> &book)
{
    for (int i = 1, j = 0; i < (int)pattern.size(); i++)
    {
        while (j && pattern[i] != pattern[j])
        {
            // 不匹配，回退到上一个相同前缀
            j = book[j - 1];
        }
        // 匹配，更新相同的前缀的最后一个index
        if (pattern[i] == pattern[j])
            j++;

        // 更新book，记录相同的前缀的最后一个index
        book[i] = j;
    }
}

int kmp(string &s, string &p, int begin)
{
    int res = -1;
    vector<int> book(p.size());

    get_backoff(p, book);

    for (int i = begin, j = 0; i < (int)s.size(); ++i)
    {
        while (j && s[i] != p[j]) // 回退p
            j = book[j - 1];
        if (s[i] == p[j])
            j++;
        if (j == (int)p.size())
        {
            res = i - p.size() + 1;
        }
    }
    return res;
}

int main(int argc, char *argv[])
{
    string s = "abskajakajkafkkakaj";
    string p = "kkakaj";

    string pre = "abskajakajkaf";

    cout << kmp(s, p, 0) << endl;
    cout << pre.size() << endl;
    return 0;
}

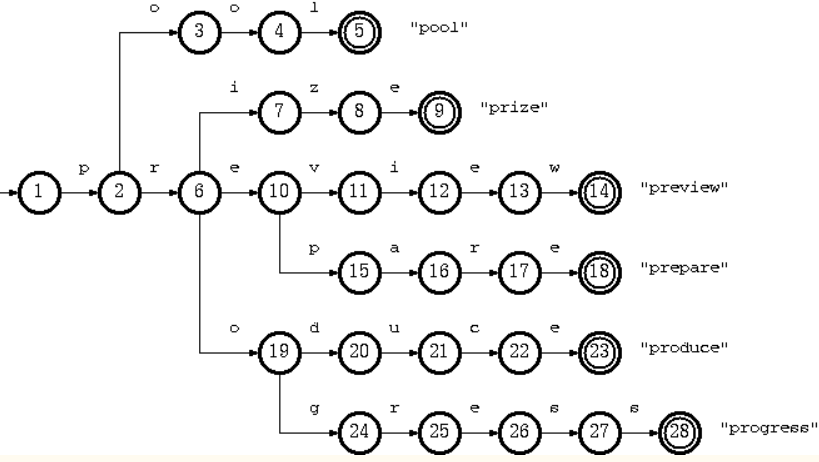
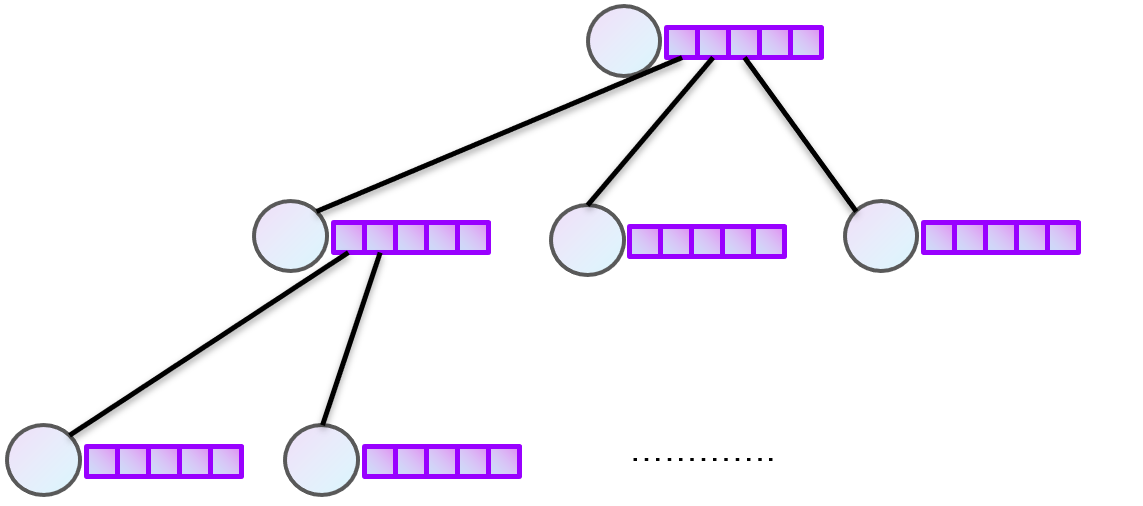
Trie前缀树或字典树

从头到尾，使用输入串中的一个字符来确定要进入的下一个状态。选择标记有相同字符的边缘以行走。每一步都消耗一个字符。

一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符。

有什么强的？

从根到叶遍历所需的时间不取决于数据库的大小，而是与键的长度成比例。因此，在一般情况下，它通常比B树或任何基于比较的索引方法快得多。它的时间复杂度与哈希技术相当。

除了效率外，在拼写错误的情况下，trie还提供了搜索最近路径的灵活性。

能做什么？

多patttern匹配

比如，你有很多个pattern，要同时在一个string s中查找，是否出现。使用Trie保存pattern，作为索引，在string中搜索，可以加快效率。

。。。

brute force需要 O(|Text| *|Patterns|)

Trie需要 O(|Text| * |Len of Longest Pattern|) 加上构造 Trie 的 O(|Patterns|)。

需要额外空间复杂度，O(|Patterns|)。

怎么实现？

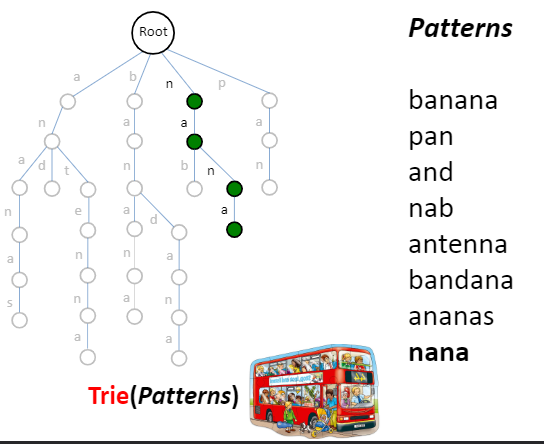
最基础的实现方式如上图。实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;

int trie[STACSIZE][N]; //手动开辟栈空间
// 或者
// vector<map<char,int>> trie[STACSIZE][N]; //手动开辟栈空间
// 或者
// vector<unordered_map<char,int>> trie[STACSIZE][N]; //手动开辟栈空间

int counts[STACSIZE];  //计数
int idx = 0;

void insert(string &s)
{
    int p = 0;
    for (int i = 0; i < s.size(); i++)
    {
        int c = s[i] - 'a';
        if (trie[p][c] == 0)
            trie[p][c] = ++idx; //没有节点，创造节点，指定在栈空间的位置
        p = trie[p][c];         //更新当前位置，进入c节点
    }
    counts[p]++; //更新计数
}

int query(string &s)
{
    int p = 0;
    for (int i = 0; i < s.size(); i++)
    {
        int c = s[i] - 'a';
        if (!trie[p][c])
            return 0;
        p = trie[p][c];
    }
    return counts[p];
}

int main(int argc, char **argv)
{
    for (int i = 0; i < 5; i++)
    {
        string s;
        cin >> s;
        insert(s);
    }

    for (int i = 0; i < 5; i++)
    {
        string s;
        cin >> s;
        cout << query(s) << endl;
    }

    return 0;
}

以上方法，就空间使用而言，这是相当奢侈的，因为在trie中，大多数节点只有几个分支，而大多数表单元格为空白。更紧凑的方案是使用链表存储每个状态的转换。但是由于是线性搜索，导致访问速度变慢。

因此，大佬设计出了快速访问的表压缩技术来解决该问题。

Double-Array Trie：包含base和check两个数组。base数组的每个元素表示一个Trie节点，即一个状态 ；check数组表示某个状态的前驱状态。

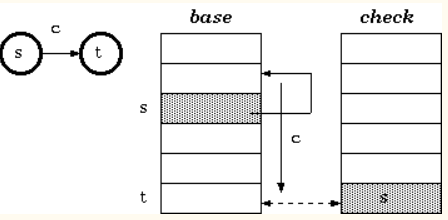
示意图所示，构造两个数组，一个base对应一个前驱check。

一步状态转移逻辑为：

t := base [ s ] + c ;

如果 check[ t ] = s， 则 next s := t

如果 check[ t ] = -s， 则 next s := t 且 t 是一个终止状态（比如表示一个词的结尾）

否则 转移失败

实现，就暂时不研究了。

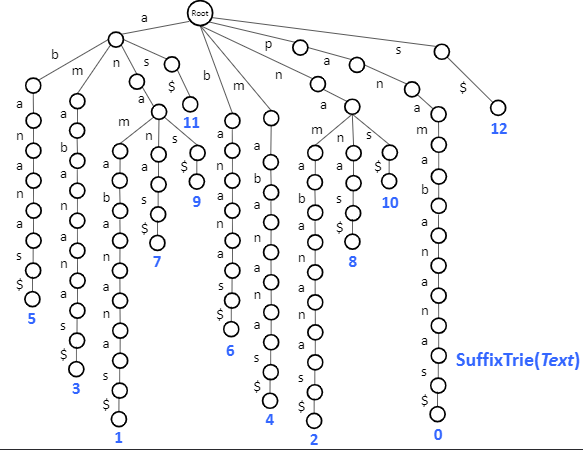
More about 多个pattern匹配

除了Trie，还有针对 string s 建树的 Suffix Trie.

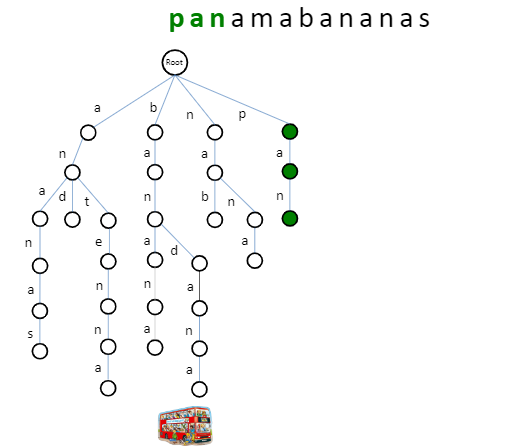
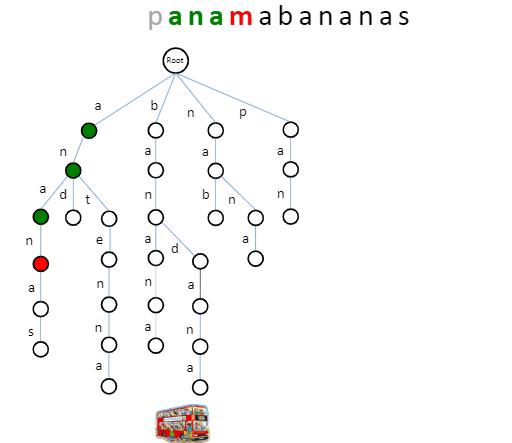
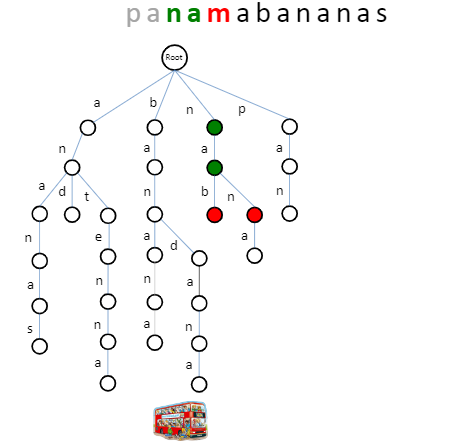
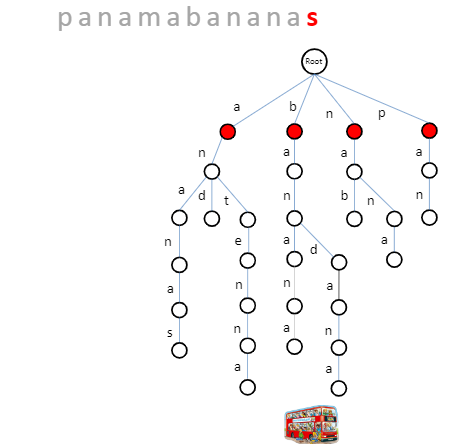
对 string：p a n a m a b a n an a s。构建后缀Trie

将 pattern 逐个输入，进行匹配。此时，不需要匹配到叶子节点。

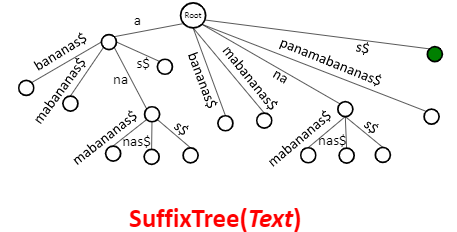
额外空间复杂度，和 string s 有关。压缩无分支后缀之后，就成了Suffix Tree。

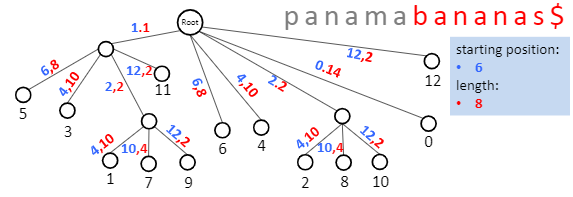
若再压缩空间，可以将suffix 变成 idx + length。

额外空间复杂度为，O(|Text|)。使用 Suffix Trie，多pattern匹配的时间复杂度为：

O(|Text| + |Patterns|)，Trie 为 O(|Text| * |Len of Longest Pattern|)。

额外空间复杂度为 O(|Text|)，Trie 为 O(|Patterns|)。只是 O(|Text|) 的系数约为20，当文本很长时，还是算了吧。

AC自动机

还是，多 pattern 匹配问题，在只是使用Trie，在string s上暴力遍历，只是寻找成功的那一刻，失败的匹配那都是没有意义的吗？

不不不，得让失败的存在，这东西越混沌，信息熵越高，有用。

AC自动机，Trie + KMP，加速多pattern匹配过程。匹配过程时间复杂度O（|Text| * Trie树高）。

  1. 构建 patterns 的 Trie
  2. 构建 fail 指针
  3. 开始匹配

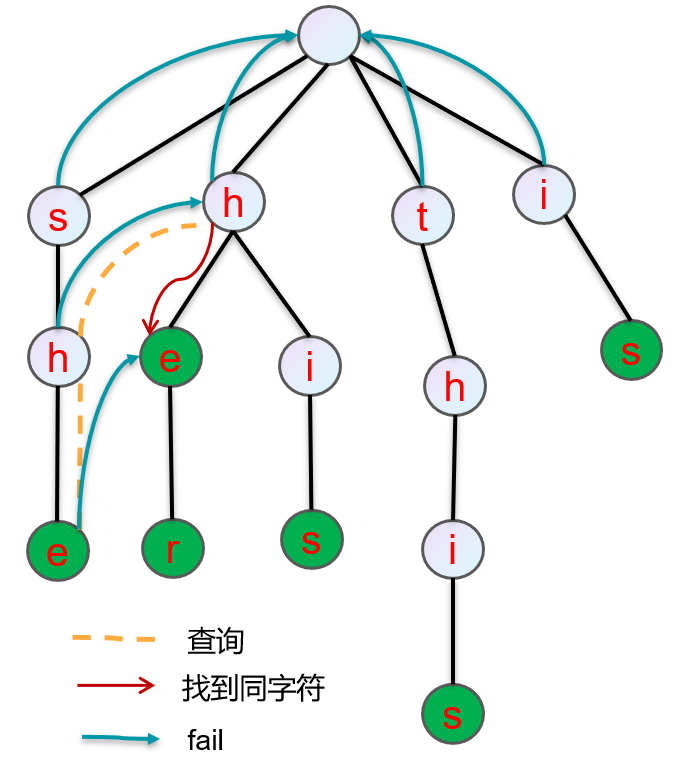
构建 fail 指针

  1. 在Trie中，BFS遍历，第一层，fail指针都指向 root
  2. 第一层之后，每个节点的 fail 指针，指向 【该节点的父节点】 的 【fail指针指向的节点】 的 【儿子节点】中 【和该节点（自己）同字符的节点】。如果没有找到，【fail指针指向的节点】继续向上找 fail 节点，直到 root。

啥是 fail ？ 当前单词的最长后缀。

匹配过程

  1. 输入string s，trie从 root开始，进行匹配
  2. 当匹配失败，跳转到fail指针指向的节点，如果fail到 root，输入此位置之后的string s的部分，继续查找。
  3. 当匹配成功（Trie标记的节点），也跳转到fail指针指向的节点，如果此时跳转到 root，进行回溯到前一个最长的trie路径节点。

跳转，就是在匹配后缀。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <bits/stdc++.h>

using namespace std;

static int idx = 0;

struct trieNode
{
    int son[26] = {0};
    int counts = 0;
    int fail = -1;
};

void insert(const string &s, vector<trieNode> &trie)
{
    int p = 0;
    for (int i = 0; i < s.size(); i++)
    {
        int cha = s[i] - 'a';
        if (!trie[p].son[cha])
            trie[p].son[cha] = ++idx;
        p = trie[p].son[cha];
    }
    trie[p].counts++;
}

void build_fail(vector<trieNode> &trie)
{
    queue<int> q;
    for (int i = 0; i < 26; i++)
    {
        if (trie[0].son[i] != 0)
        { //儿子节点
            int son = trie[0].son[i];
            trie[son].fail = 0; //第一层 fail
            q.push(son);
        }
    }

    while (q.size())
    {
        int father = q.front();
        q.pop();
        for (int i = 0; i < 26; i++)
        {
            if (trie[father].son[i] != 0)
            {
                int cur = trie[father].son[i];        // 要找fail的儿子
                int failOfFather = trie[father].fail; // 父节点的fail
                // ~(0): -1,   ~(-1): 0
                //不是根节点且没有找到目标同字符
                while (~failOfFather && !trie[father].son[i])
                    failOfFather = trie[failOfFather].fail;

                if (~failOfFather) //找到目标同字符
                    trie[cur].fail = trie[failOfFather].son[i];
                else // 根节点
                    trie[cur].fail = 0;
                q.push(cur);
            }
        }
    }
}

int query(const string &s, vector<trieNode> &trie)
{
    int ans = 0;
    int ptr = 0;
    for (int i = 0; i < s.size(); i++)
    {
        int word = s[i] - 'a';
        // 儿子不存在且fail不是根节点，跳转 fail
        while (!trie[ptr].son[word] && ~trie[ptr].fail)
            ptr = trie[ptr].fail;
        if (trie[ptr].son[word]) // 儿子存在，匹配，进入节点，继续查找
            ptr = trie[ptr].son[word];
        else // 是根节点，下一个 s 字符
            continue;

        int ptr_temp = ptr;          // copt ptr，ptr为回溯位置
        while (~trie[ptr_temp].fail) //到根节点退出，下一个外层for回溯
        {
            ans += trie[ptr_temp].counts; // counts在不是目标处为0
            ptr_temp = trie[ptr_temp].fail;
        }
    }
    return ans;
}

int main(int argc, char **argv)
{
    vector<trieNode> trie;
    trie.resize(50);

    insert("she", trie);
    string s = "he";
    insert(s, trie);
    insert("her", trie);
    insert("is", trie);
    insert("this", trie);
    insert("his", trie);

    build_fail(trie);

    cout << query("sherthis", trie) << endl;
}