Transformer Model
1.Transformer模型
序列计算中,传统的RNN在预测下一个符号(token)的时候,会对以往的历史信息有很强的依赖,使得难以充分地并行化,也无法很好地加深网络的层级结构。
而对于传统的基于CNN的神经机器翻译模型,两个任意输入与输出位置的信号关联所需要的运算数量与它们的位置距离成正比,Facebook提出的CNN NMT 为线性增长。
这两种常见的结构使得学习较远位置的依赖关系(long-term dependency)非常困难。
在 Transformer 中,两个任意输入的信号关联的开销会减少到一个固定的运算数量级,使用 Multi-Head Attention 注意力机制可以完全脱离RNN及CNN的结构,使得Transformer可以高效地并行化,并堆叠多层的网络。
自注意力(Self-attention),是一种涉及单序列不同位置的注意力机制,并能计算序列的表征。自注意力这种在序列内部执行 Attention 的方法可以视为搜索序列内部的隐藏关系,这种内部关系对于翻译以及序列任务的性能非常重要。
1.1 编码器 encoder
编码器encoder由6层结构一样的网络层组成,每一层有2个子层:
第一个子层是multi-head self-attention Layer
第二个子层是一个基于位置编码的全连接网络层(position-wise fully connected feed-forward network)
会使用残差连接的方式,分别对每个子层的输入加到这个子层的输出上,然后再接一个Layer normalization的归一化层。
\[ \text{LayerNorm}(x+\text{Sublayer}(x)) \]
所有的embedding及hidden state的维度都是512
1.2 解码器 decoder
解码器decoder由6层结构一样的网络层组成,每一层除了跟encode人一样有2个子层以外,还有第3个子层
- 第一个子层是multi-head self-attention Layer
- 第二个子层是一个基于位置编码的全连接网络层(position-wise fully connected feed-forward network)
- 第三个子层用于对encoder的输出向量进行multi-head attention
- 同样的,会使用残差连接的方式,然后再接一个Layer normalization的归一化层。 \[ \text{LayerNorm}(x+\text{Sublayer}(x))\\ \]
- decoder还需要将还没有生成的后续序列掩盖(masking),这样做是为了防止decoder在做self-attention的时候关注到后续还未生成的单词上去。
1.3 注意力机制
- 传统的注意力机制,也称为scaled Dot-Product Attention,可以看成是有一个询问的词(query),去跟一堆哈希表中的键值对(key-value pair)进行匹配,找到最相关的键(key),之后返回该键所对应的值(value)。通常的,如果只返回一个key所对应的value,称之为hard attention。如果对所有的key都计算一个相关系数,(也称之为attention weight),可以将所有key对应的value进行加权求和(weighted sum)这样的操作称之为soft attention。 \[\text{Attention}(Q,K,V) = \text{softmax}\left({QK^T \over \sqrt{d_k}}\right)V\]
- 其中所有的query和key都是维度为\(d_k\)的向量,将这些向量分别叠在一起形成 \(Q\in\mathbb{R}^{|Q|\times d_k}, K\in\mathbb{R}^{|K|\times d_k}\)的矩阵。
- 所有的value都是维度为\(d_v\)的向量,将这些向量叠在一起形成\(V\in\mathbb{R}^{|V|\times d_k}\)
- 这里如果维度\(d_k\)很大的时候,两个向量的乘积会变得很大,使得softmax会得到非常小的数值,所以会在这里除以\(\sqrt{d_k}\)来抵消这个影响。
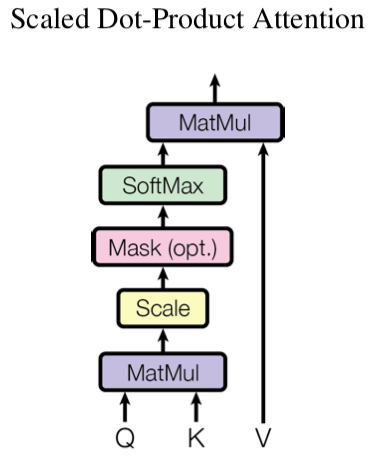
1.4 Multi-Head Attention
这里假设\(Q,~K,~V\in \mathbb{R}^{d_\text{model}}\)都在一个\({d_\text{model}}\)维度的空间中
使用h个不一样权重的线性映射函数\((QW^Q_i, KW^K_i, VW^V_i)\)将Q, K, V分别映射到\(d_k,~d_k,~d_v\)空间中
对映射之后的Q, K, V 做h次attention,并将h个attention head连接在一起形成一个新的向量
最后再将这个向量映射到\(d_\text{model}\)空间,作为下一层的输入
\[ \text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1,\cdots, \text{head}_h) W^O \\ \text{head}_i = \text{Attention}(QW^Q_i, KW^K_i, VW^V_i) \]
其中\(W^Q_i\in \mathbb{R}^{d_\text{model}\times d_k}, W^K_i\in \mathbb{R}^{d_\text{model}\times d_k}, W^V_i\in \mathbb{R}^{d_\text{model}\times d_v}, W^O\in \mathbb{R}^{hd_v\times d_\text{model}}\), 常见的设置\(h=8,d_k=d_v=d_\text{model}/h=64\)
模型图
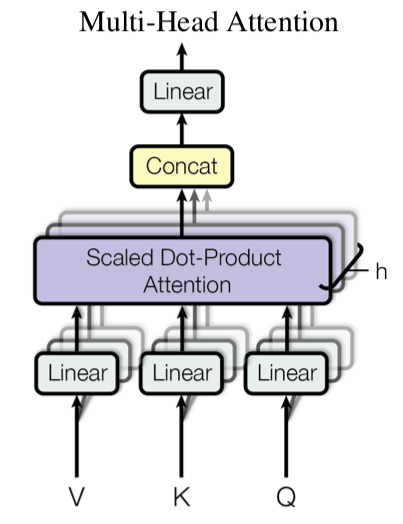
应用
- 将decoder上一个时刻的hidden state 作为query,将encoder的最顶层的所有输出的hidden state作为key和value,这样可以类似传统的attention机制一样去发现源语言单词与目标语言单词之间的联系
- encoder本身会对源语言单词进行multi-head self attention,其中query,key,value都是一样的,都是上一层中输出的单词的hidden state,每一个时刻计算出来的context vector都会作为该层输出的新的单词的hidden state,并作为下一层的输入。
- decoder本身也会类似encoder一样去做self attention,不同的是,decoder只对左边已经生成的序列进行attention,对还没有生成的(右边的)序列掩盖(masking)
完整的模型图
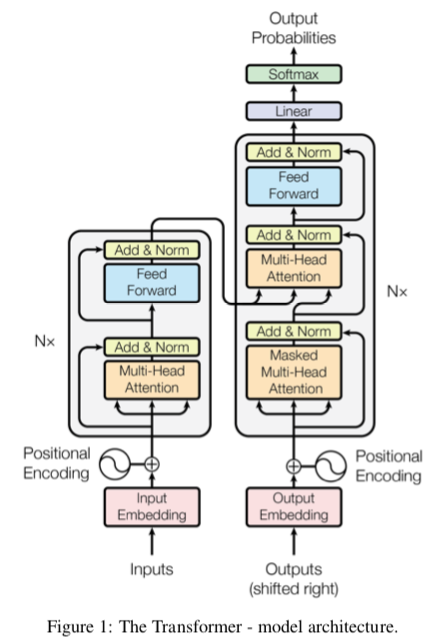
1.5 基于位置的前向神经网络(Position-wise Feed-Forward Networks)
- 对于encoder和decoder的每个attention层之后,还会在连接一个全连接的前向神经网络。这个网络包含了两个线性转换和中间加一个ReLU的激活函数 \[FFN(x) =\max(0, xW_1+b_1) W_2+b_2\]
- 这里每一层,都用不同的\(W_1,W_2,b_1,b_2\)。
1.6 词向量矩阵及Softmax层
- 这里使用常见的词向量矩阵,并encoder会把词向量映射到\(d_\text{model}\)空间上,作为第一层的输入
- 在做预测的时候,会将输出向量映射到一个词表大小的概率空间中,并使用softmax来归一化到一个\([0,1]\)之间的概率值。
1.7 位置编码(position embeddings)
因为模型没有recurrence及convolution的操作,所以为了让模型能够分辨不同位置的单词,需要对单词的位置进行编码。
\[PE(pos, 2i)=\sin(pos/10000^{2i/d_\text{model}}) \\ PE(pos, 2i+1)=\cos(pos/10000^{2i/d_\text{model}})\]
pos是这个单词在句子中的位置,i是这个位置向量的第i个维度的编号。这样的波长形成了一个从\(2\pi\)到\(1000\cdot 2\pi\)的几何级数。这样会使得模型更容易学到相对距离,因为\(PE_{pos+k}\)可以表示为\(PE_{pos}\)的一个线性变化。
1.8 Transformer 对比RNN及CNN
- 发现RNN需要进行\(O(n)\)个序列操作,而Transformer和CNN只需要\(O(1)\)个
- CNN会形成一个层级结构,类似树状,所以任意两个单词到达的最大路径长度是\(O(\log_k(n))\)
- 如果self-attention只对该单词周围r个单词进行attention操作,可以得到restricted版本的self-attention,
这样可以减少每一层的计算复杂度,但未增加两个任意词之间到达的最长路径。

2. Transformer模型的训练细节
- 优化方法
- 正则化 (regularization)
- label smoothing
2.1 优化方法
- Adam 优化方法,\(\beta_1=0.9, \beta_2=0.98, \epsilon=10^{-9}\)
- learning rate是随着训练的过程中,通过以下一个函数进行变化。一开始在前 warmup_steps个训练迭代中learning rate是线性增长的,往后随着步长的增加而下降。 一般会设置 warmup_steps = 4000 \[lr = d_\text{model}^{-0.5} \cdot \min(\text{step_num}^{-0.5},\text{step_num}\cdot \text{warmup_steps}^{-1.5}) \]
2.2 正则化 Regularization
- 对每一个子层的输出,在该子层的输出加上该子层的输入之前进行dropout
- 对encoder及decoder,词向量和位置向量求和之后都进行dropout
2.3 Label Smoothing
- 对于正确的标注label,在其one-hot表达上,加上一个均匀分布的向量,这个smoothing的数值是\(\epsilon_{ls}=0.1\)
3 Tranformer Code
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!